分析：

规律：
题目中给定条件：
1. 能量石会随着时间流逝逐渐失去能量
2.能量石中包含的能量最多降低至0。
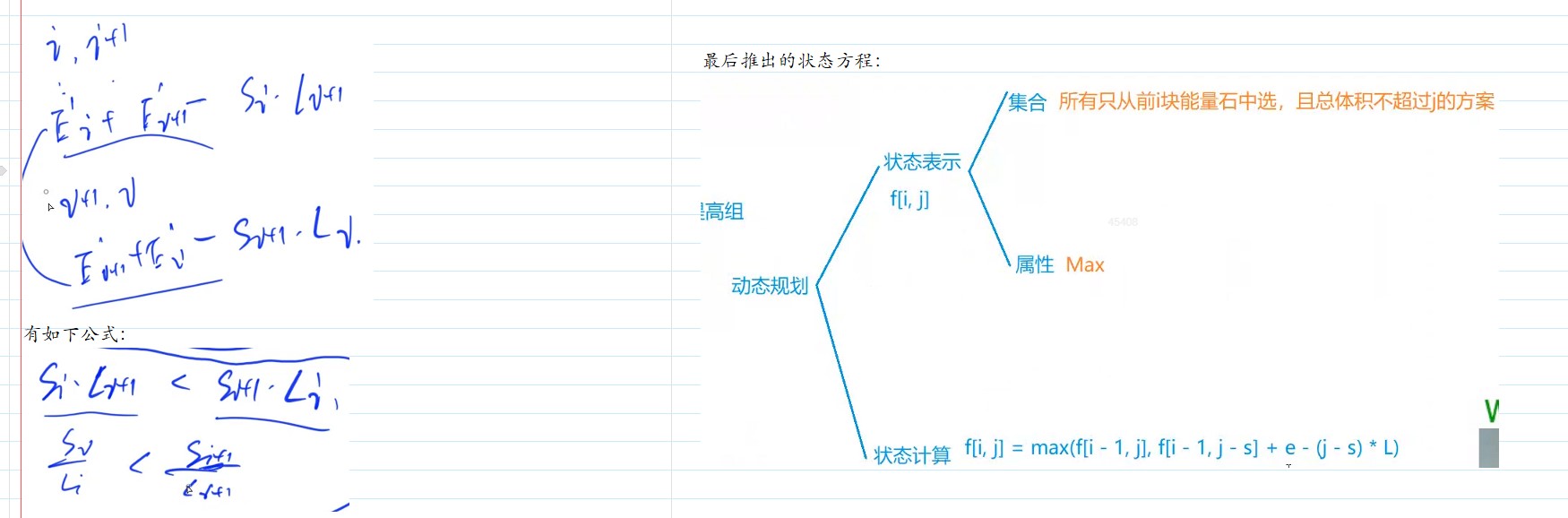
因此，先枚举所有所有选法，贪心思路发现i和I + 1物品之间的联系，通过这种联系排好序之后，确定为0/1背包（枚举了所有的选法，从中找到了最大值）。

思路：
首先因为最低降到0，所以降到0等价于不选，所以等价于从“先枚举选哪些，再枚举每种选法的顺序”所得到的所有方案中取最大值。
然后我们发现一定存在一组最优解，使得在每个选法中，顺序是特定的.
因此我们只需要考虑所有排好序的方案即可，所以当所有能量石排好序后，我们只需考虑选法即可，所以用01背包问题可以解决。

$\cal{Question}$:
为什么是恰好是而不是最多是？
$\cal{Ans}$:
if(e > (j - s)* l) f[j] = max(f[j], f[j - s] + e - (j - s) * l);
这段话出现了：j增大的时候，如果能量石的能量消耗完，后面是不计算的，因此最后f[m]不不一定是最大值。所以不管是恰好是而不是最多是，都要循环一遍求最值

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 10010;
int f[N];
struct stone
{
    int s, e, l;
    bool operator< (const stone & w)const 
    {
        return s * w.l < w.s * l;
    }
}S[N];

int main()
{
    int T; cin>> T;
    for(int C = 1; C <= T; ++C)
    {
        int n, m = 0; cin >> n;
        for(int i = 1; i <= n; ++i)
        {
            int s, e, l; cin>> s >> e >> l;
            S[i] = {s, e, l};
            m += s;
        }
        memset(f, 0, sizeof f);
        f[0] = 0;
        /*根据贪心思想排序*/
        sort(S + 1, S + n + 1);
        /*0/1背包*/
        for(int i = 1; i <= n; ++i)
        {
            int s = S[i].s , e = S[i].e, l = S[i].l;
            for(int j = m; j >= s; j--)
               if(e > (j - s)* l) f[j] = max(f[j], f[j - s] + e - (j - s) * l);
        }
        int res= 0;
        for(int i = 1; i <= m; ++i)res = max(res, f[i]);
        printf("Case #%d: %d\n",  C,res);
    }

    return 0;
}