$\color{red}{初等行列变化:\\\\ 1.某一行乘上一个非零数,矩阵不变 \\\\ 2.某一行乘上一个常数加到另一行上,矩阵不变 \\\\ 3.交换矩阵中某两行的元素,矩阵不变}$
思路:利用$\color{red}{初等行列变化}$将矩阵变换成上三角形矩阵,再由后往前推出解
上三角形矩阵带来的结果有三种:无解,有唯一解,无穷多解
$\color{blue}{无解:若在最后化成的上三角形矩阵中,正对角线中某个元素为0,但其所在行的最后一列元素不为0时,\\\\此时矩阵无解}$
$\color{blue}{有无数解:若在最后化成的上三角形矩阵中,存在正对角线中某个元素为0,且其所在行的最后一列元素\\\\也为0时,此时矩阵有无穷组解}$
$\color{blue}{有唯一解:若在最后化成的上三角形矩阵中,不存在正对角线中某个元素为0,此时矩阵有唯一解}$
矩阵的解想要更深入了解可以看下大学的线性代数

高斯消元步骤:

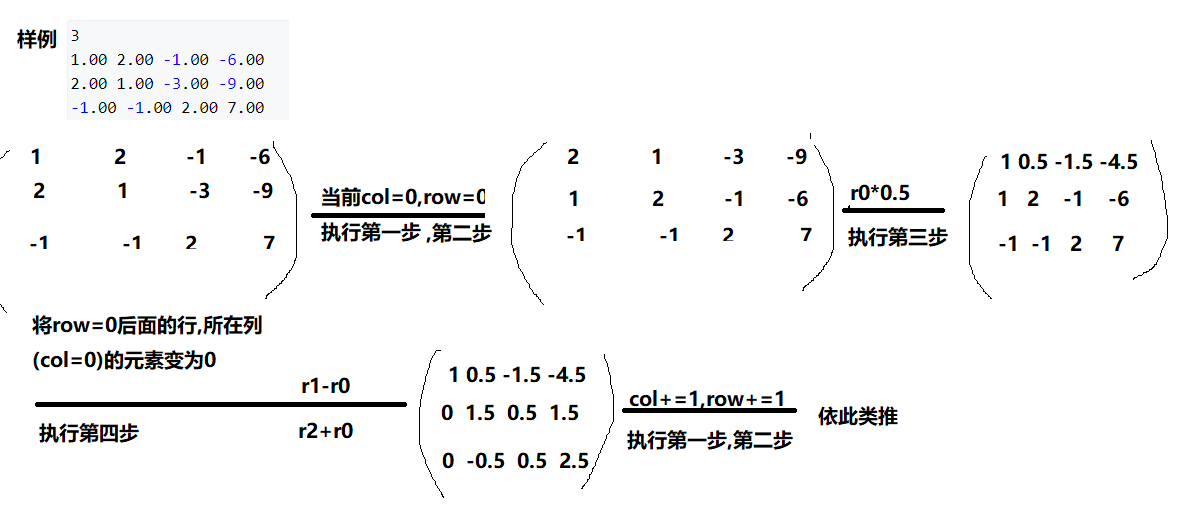
1.筛选出所在列元素最大的行
2.将步骤1筛选出的行与所在行进行交换
3.将所在行所在列元素变为1
4.将所在行所在列的后面行的所在列元素变为0

高斯消元版本一 $\quad O(n^3)$

#include<iostream>
#include<cmath>
using namespace std;
const int N=110;
const double zero=1e-6;
int n;
double a[N][N];
int gauss()
{
    int row,col;
    for(row=0,col=0;col<n;col++)
    {
        int t=row;//所在列元素最大值的行索引
        //1.筛选出所在列元素最大的行
        for(int i=row;i<n;i++)
            if(a[i][col]>a[t][col]) t=i;
        //正对角线中有元素为0,这时有无穷解和无解的依据
        //不计算该行
        if(fabs(a[t][col])<zero) continue;
        //2.将步骤1筛选出的行与所在行进行交换
        for(int i=col;i<=n;i++) 
            swap(a[t][i],a[row][i]);
        //3.将所在行所在列元素变为1
        //必须要逆序,如果正序,会修改a[row][col]的值
        //后续元素除的a[row][col]就是后来修改后的
        //a[row][col],而不是之前的a[row][col]
        for(int j=n;j>=col;j--)
            a[row][j]/=a[row][col];
        //4.将所在行所在列的后面行的所在列元素变为0
        for(int i=row+1;i<n;i++)
            if(fabs(a[i][col])>zero)
                for(int j=n;j>=col;j--)//逆序的道理同
                    a[i][j]-=a[row][j]*a[i][col];
        row++;
    }
    //row<n,即对角线中元素为0的行未被算上,此时有
    //无解和无穷组解两种结果
    if(row<n){
        for (int i = row;i<n;i++)
            if (fabs(a[i][n]) > zero)
                return 0;//无解
        return 2;//无数穷组解
    }
    //唯一解,从下往上计算解
    for(int i=n-1;i>=0;i--)
        for(int j=i+1;j<n;j++)
            a[i][n]-=a[j][n]*a[i][j];
    return 1;
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n+1;j++)
            cin>>a[i][j];
    int flag=gauss();//0代表无解,1代表有一个解,2代表有无数解
    if(flag==1)
        for(int i=0;i<n;i++) printf("%.2lf\n",a[i][n]);
    else if(flag==2) printf("Infinite group solutions\n");
    else printf("No solution\n");
}

高斯消元版本二 $\quad O(n^3)$

#include<iostream>
#include<cmath>
using namespace std;

const int N = 110;
const double zero = 1e-6;
double a[N][N];
int n;
int gauss()
{
    //处理矩阵
    //枚举列
    int r=0;
    for(int j=0;j<n;j++)
    {
        //当前列元素最大值的行索引
        int t = r;

        //枚举当前列其他行,选出当前列元素最大值的行索引
        for(int k = r+1;k<n;k++)
            if(a[k][j]>a[t][j]) t=k;//如果当前列的第k行元素大于设定的当前列第t行的元素,更新最大索引

        for(int k = j;k<=n;k++)
            swap(a[t][k],a[r][k]);

        //将当前列元素最大所在行的元素变为1 因为除数不能为0,若除数为0,说明当前列,已经满足上三角形类型
        if(fabs(a[r][j])<zero) continue;
        for(int k=n;k>=j;k--)   a[r][k]/=a[r][j];

        //将当前列除第r行外,其他行的元素变为0
        for(int k=r+1;k<n;k++)
            for(int l = n;l>=j;l--)
                a[k][l]-=a[k][j]*a[r][l];
        r++;
    }
    //无解和无穷组解
    if(r<n)
    {
        for(int i=r;i<n;i++)
            if(fabs(a[i][n])>zero)
                return 0;
        //如果不是无解,那么就是无穷多组解
        return 2;
    }
    //存在唯一解,逆序回去
    for(int i=n-1;i>=0;i--)
        for(int j = i+1;j<=n;j++){
            a[i][n]-=a[j][n]*a[i][j];
        }
    return 1;
}
int main()
{
    cin>>n;
    //读入矩阵
    for(int i=0;i<n;i++)
        for(int j=0;j<=n;j++)
            cin>>a[i][j];
    cout.setf(ios_base::fixed);
    cout.precision(2);
    int flag = gauss();
    if(!flag) cout<<"No solution";
    else if(flag%2) for(int i=0;i<n;i++) cout<<a[i][n]<<endl;
    else cout<<"Infinite group solutions";
}

$\color{brown}{喜欢题解的话,欢迎点赞、收藏、关注(三连)喔,如有什么疑问,欢迎评论下方指出}$