题目描述

设有N堆石子排成一排，其编号为1，2，3，…，N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这N堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有4堆石子分别为 1 3 5 2， 我们可以先合并1、2堆，代价为4，得到4 5 2， 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24；

如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式

第一行一个数N表示石子的堆数N。

第二行N个数，表示每堆石子的质量(均不超过1000)。

输出格式

输出一个整数，表示最小代价。

数据范围

1≤N≤300

输入样例

4
1 3 5 2

输出样例

22

算法1 区间DP

这道题因为一次合并相邻的两堆石子,相当于一次合并相邻的两个区间,所以采用了区间DP的方式.
区间DP就是在定义状态时定义了一个区间.
首先对这道题进行集合的划分:

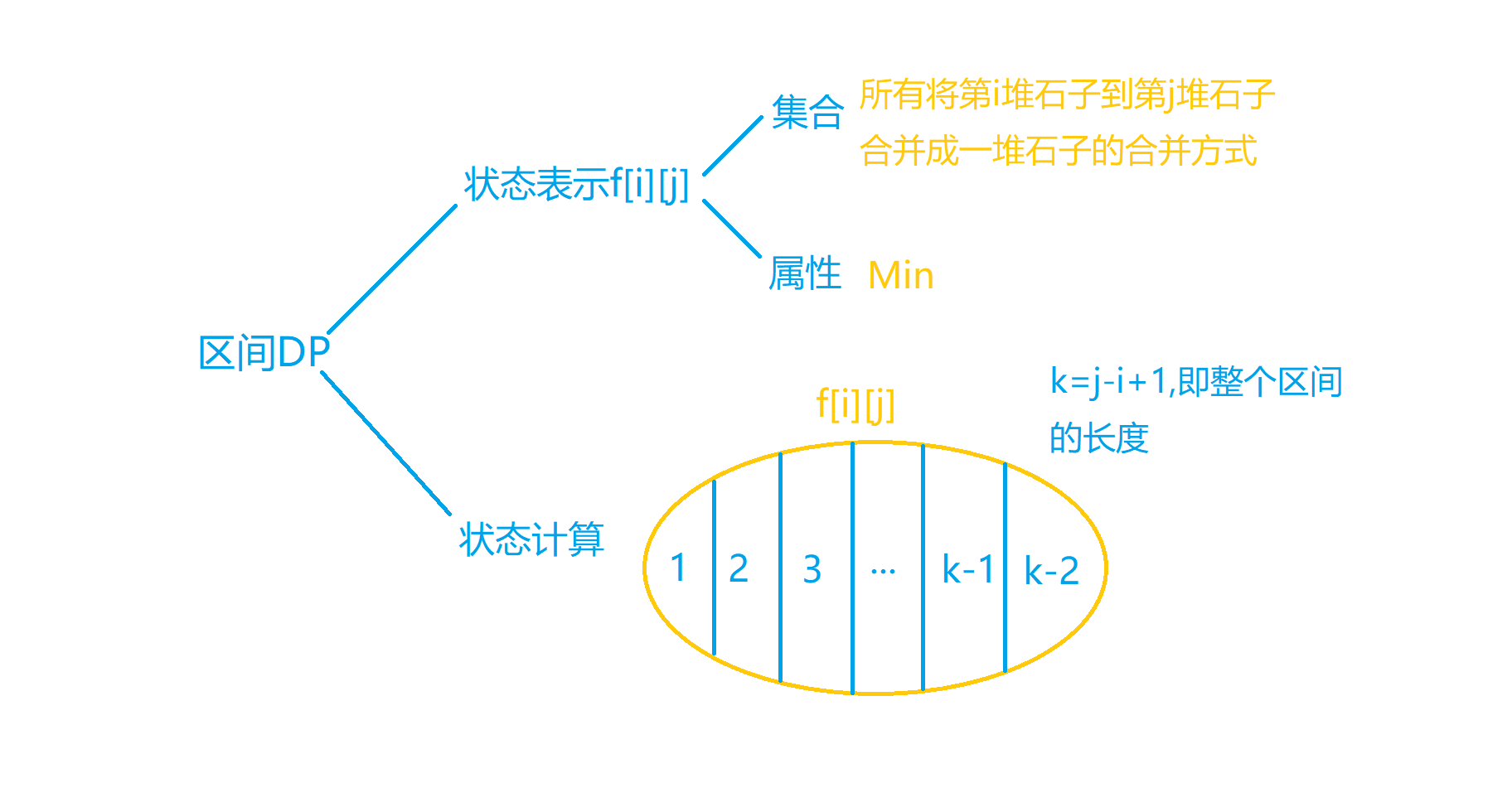
我们需要思考的是在确定集合为将i到j堆石子合并的方式之后,需要考虑应该如何对这个集合进行划分,使得其是我们可以表示出来的.我们可以发现一个规律,不管集合是如何划分的,最后一定会剩下2堆,然后把这两堆合并成一堆.所以我们可以以最后一次合并的分界线的位置来进行集合的分类,如下图所示:

我们将集合分成若干类是以最后一步时是将左边的哪一部分与右边的哪一部分进行了合并,以这个分界线来分类,总共的代价就是每一类的最小代价再取一个min,每一步的最小代价就是左边的最小代价加上右边的最小代价再加上最后一步的最小代价.

时间复杂度

状态数量是两维的$O(n^2)$,状态的计算是需要枚举一个k,k是$O(n)$的一个计算量
所以总体的时间复杂度为$O(n^3)$.

代码思路

实际在代码实现的时候按照长度从小到大枚举了所有状态,这是为了保证每一个用到的状态都被提前计算过.
区间长度len的意思是选定的区间有多长,i表示起点即左端点如

n = 4;
len = 2; i=1, i<=3, i++;
len = 4; i=1; i<=1, i++;

这里的len和i意义是什么,为什么要这么写,如下图所示:

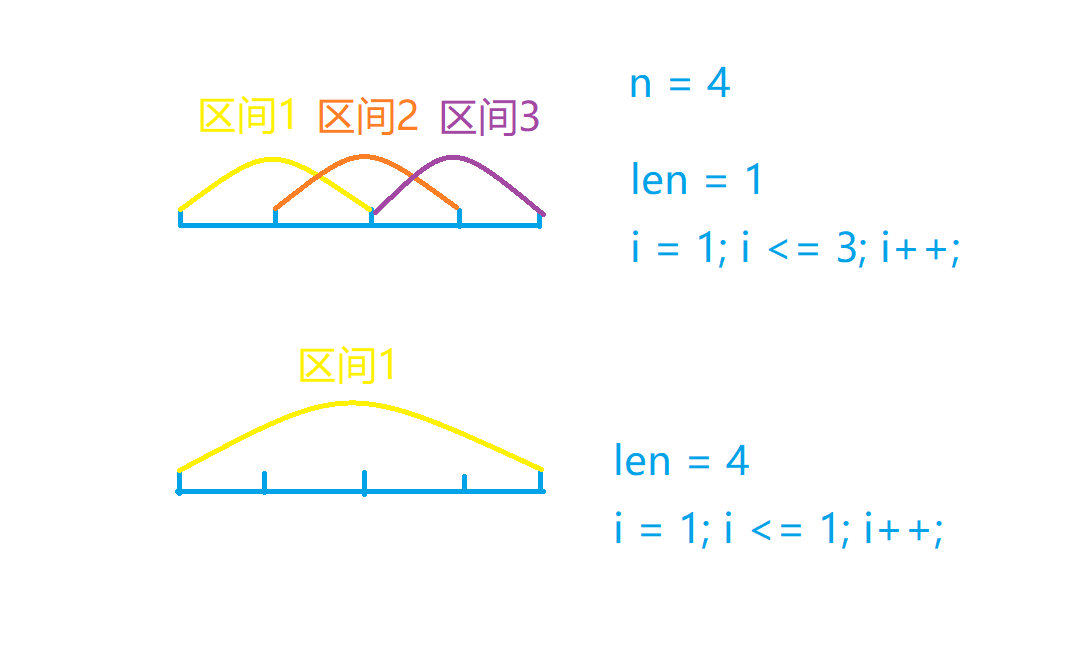
如果有4个石子,len=2的意义是每次选定合并区间长度为2,所以i=1,2,3

C++ 代码

#include<iostream>

using namespace std;

const int N = 1010;
int s[N]; // 前缀和
int f[N][N];

int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> s[i];

    // 计算前缀和
    for(int i = 1; i <= n; i++) s[i] += s[i-1];

    // 枚举所有状态
    // 长度从小到大来枚举所有状态
    // 区间长度为1时合并不要代价,所以区间长度从2开始
    for(int len = 2; len <= n; len++)
    // 枚举完长度枚举一下起点
        for(int i = 1; i <= n-len+1; i++)
        {

            int l = i, r = i + len -1; 
            // 因为是取min值,所以先将f[l][r]置为无穷
            f[l][r] = 0x3f3f3f3f;
            // 枚举一下分界点,构造状态转移方程
            for(int k = l; k < r; k++) // k从l到r-1
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        }
    cout << f[1][n] << endl;
    return 0;
}