分析:
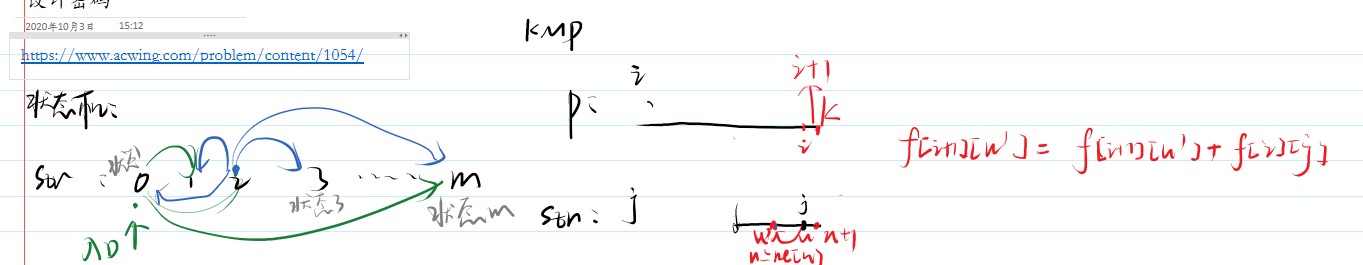
分析:
题目中不包含子串可以转换成KMP中字串s走不到p字符串中最后一个点的方案数
即:
1.每设计一位密码,都把从1~i(当前位)的密码 P当成KMP中的主字符串, 给的字符串str是KMP中的子字符串.
2.如果str在 P 中的KMP匹配中,str的匹配下标j到达m(j == m)说明,str在P中。因此,如果走不到,说明P中没有str。
3.转换成状态机:状态机中的状态i就是表示 进行KMP匹配的子字符串 str[0] ~ str[i], 当I == m 的时候,走到了状态m
每个点都可能有26种选择, 一共m + 1个点。
复杂度:m * 26 * N
状态定义和方程:
f[I , j ]: 父字符串P中枚举到了第i个位置(0 ~ i), 并且和子字符串T(0 ~ j)KMP匹配的方案数。
状态方程:
当前点能够更新的状态(f[I + 1, u]) = 当前点的状态(f[I , j])+ 更新点原本的状态(f[I + 1, u])
从状态机的角度来说:
当前状态方案数 = 从上一个状态跳转道这个状态的方案数 + 自己原本的方案数
f[I + 1, u] = f[I + 1, u] + f[I , j]
j: 枚举到子字符串0~j
U: 子字符串 0 ~ u 在父字符串中出现过。
I + 1: 父字符串枚举到了0~I + 1
步骤:
1.求str的next数组。
next[i] = j 表示下标以i-j为起点,i为终点的后缀和下标以0为起点,j为终点的前缀相等,
且此字符串的长度最长。即有 str[1 ~ j] 和 str[I - j + 1 ~ i]相等。
2.给定了要求的主字符串的长度,遍历每一位。
由于状态方程的关系:每次求的是 I + 1,原来是求 字符串P[1 ~ n], 下标就要从 0 ~ n - 1。
3.遍历子字符串
4.P的每一位取值是 a ~ z, 因此str中的每一位都要和a ~ z作比较,如果不相等跳回next数组, 相等就跳到下一个状态。
代码:
$\cal{o(26 * n^3)}$
#include<iostream>
#include<cstring>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 60, mod = 1e9 + 7;
int f[N][N], ne[N];
char str[N];
int main()
{
int n;
char T[N]; cin >> n >> T + 1;
/*更新ne*/
int m = strlen(T + 1);
for(int i = 2, j = 0; i <= m; ++i)
{
while(j && T[i] != T[j + 1])j = ne[j];
if(T[i] == T[j + 1])j++;
ne[i] = j;
// cout << i << ' ' << ne[i] <<endl;
}
f[0][0] = 1;
for(int i = 0; i < n; ++i)
{
/* int u = j;
while(u && str[i] != T[u + 1])u = ne[u];
if(str[i] == T[u + 1])u++;
cout << u << endl;
if(u < m)f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;*/
for(int j = 0; j < m; ++j)
{
for(char k = 'a'; k <= 'z'; ++k)
{
int u = j;
while(u && T[u + 1] != k)u = ne[u];
if(T[u + 1] == k)u++;
// cout << u << endl;
if(u < m)f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
}
}
}
int res = 0;
for(int i = 0; i < m; ++i)
res = (res + f[n][i]) % mod;
cout <<res <<endl;
return 0;
}
预处理方式:$\cal{o(26 * n^2)}$
#include<iostream>
#include<cstring>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 60, mod = 1e9 + 7;
int f[N][N], ne[N], e[N][N];
char str[N];
int main()
{
int n;
char T[N]; cin >> n >> T + 1;
/*更新ne*/
int m = strlen(T + 1);
for(int i = 2, j = 0; i <= m; ++i)
{
while(j && T[i] != T[j + 1])j = ne[j];
if(T[i] == T[j + 1])j++;
ne[i] = j;
// cout << i << ' ' << ne[i] <<endl;
}
f[0][0] = 1;
/*预处理*/
for(int u = 0; u < m; ++u)
{
for(int k = 'a'; k <= 'z'; ++k)
{
int i = u;
while(i && T[i + 1] != k)i = ne[i];
if(T[i + 1] == k)i++;
e[u][k - 'a'] = i;
}
}
/*为什么ij要从0开始?*/
/*为什么不能 取到 n, m?*/
/*由于状态方程的关系:每次求的是 I + 1,原来是求 字符串P[1 ~ n], 下标就要从 0 ~ n - 1。*/
for(int i = 0; i < n; ++i)
{
for(int j = 0; j <= m; ++j)
for(char k = 'a'; k <= 'z'; ++k)
{
int u = e[j][k- 'a'];
// cout << u << endl;
if(u < m)f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
}
//j++;
}
int res = 0;
for(int i = 0; i < m; ++i)
res = (res + f[n][i]) % mod;
cout <<res <<endl;
return 0;
}

