题目描述

每当用户执行变更文件夹操作时，LeetCode 文件系统都会保存一条日志记录。

下面给出对变更操作的说明：

• "../"：移动到当前文件夹的父文件夹。如果已经在主文件夹下，则 继续停留在当前文件夹。
• "./"：继续停留在当前文件夹。
• "x/"：移动到名为 x 的子文件夹中。题目数据 保证总是存在文件夹 x。

给你一个字符串列表 logs，其中 logs[i] 是用户在第 i 步执行的操作。

文件系统启动时位于主文件夹，然后执行 logs 中的操作。

执行完所有变更文件夹操作后，请你找出 返回主文件夹所需的最小步数。

样例

输入：logs = ["d1/","d2/","../","d21/","./"]
输出：2
解释：执行 "../" 操作变更文件夹 2 次，即可回到主文件夹

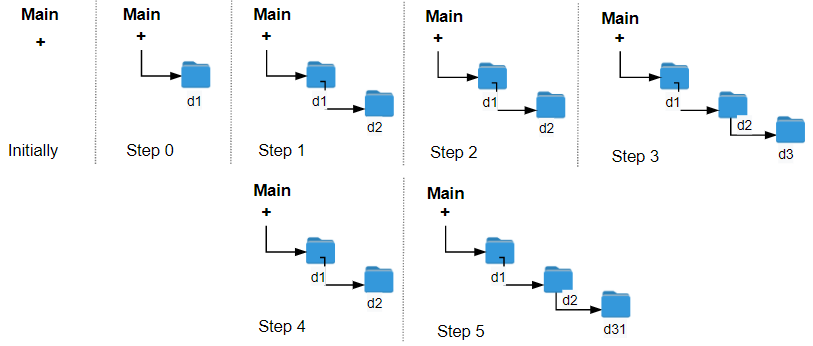
输入：logs = ["d1/","d2/","./","d3/","../","d31/"]
输出：3

输入：logs = ["d1/","../","../","../"]
输出：0

限制

• 1 <= logs.length <= 10^3
• 2 <= logs[i].length <= 10
• logs[i] 包含小写英文字母，数字，'.' 和 '/'。
• logs[i] 符合语句中描述的格式。
• 文件夹名称由小写英文字母和数字组成。

算法

(模拟) $O(n)$

1. 用一个计数器记录当前与根目录的距离。
2. 遇到 './'，则忽视本次操作。遇到 '../' 则计数器减 1，注意最小为 0。否则计数器加 1。

时间复杂度

• 遍历日志列表一次，故总时间复杂度为 $O(n)$。

空间复杂度

• 仅需要常数的额外空间。

Go 代码

func minOperations(logs []string) int {
    var res int
    for _, log := range logs {
        if log == "./" {
            continue
        }

        if log == "../" {
            res--
        } else {
            res++
        }
        if res < 0 {
            res = 0
        }
    }
    return res
}