该种方法适合在稠密图中使用
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=510;
int n,m;
int dist[N],g[N][N];//dist存储的是最短的距离,g存储的是邻接矩阵
bool st[N];//表示该点是否已经确定了最短距离
int dijkstra()
{
memset(dist,0x3f,sizeof(dist));//初始化距离
dist[1]=0;//起点到起点的距离为0
for(int i=1;i<n;i++)//因为每次循环中都可以确定一个最短距离的点,因为总共有n个点,1这个点的距离已经确定了,所以循环n-1次
{
int t=-1;//t=-1的作用是可以找出第一个点
for(int j=1;j<=n;j++)//第一轮循环,寻找与起点最短距离的点
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
st[t]=true;//标记该点的最短距离已经确定了,然后用确定的点更新其他点的最短距离
for(int j=1;j<=n;j++)//第二轮循环,用已经确定了的最短距离的点来更新到其他点的最短距离
dist[j]=min(dist[j],dist[t]+g[t][j]);
//比较 起点到j的距离 和 起点到t的距离加上t到j的距离;
}
if(dist[n]==0x3f3f3f3f) return -1;//如果n到起点的距离为0x3f说明走不到n这个点
//注:不能写成0x3f,只有清空操作时才能用0x3f,其他操作时需要写成0x3f3f3f3f,否则会报错
else return dist[n];//返回起点到n的最短距离
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof(g));//将所有边的权值更新为一个非常大的数字
while(m--)//输入边与边之间的权值
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=min(g[a][b],c);//可能存在重边,而本题追求的是最短距离,所以选择重边中最短的那条边
}
int t=dijkstra();
printf("%d\n",t);
return 0;
}


nb
#include [HTML_REMOVED]
#include [HTML_REMOVED]
#include [HTML_REMOVED]
using namespace std;
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
}
int main()
{
scanf(“%d%d”, &n, &m);
}
/作者:yxc
链接:https://www.acwing.com/activity/content/code/content/48488/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。/
大佬,为什么代码里没有处理自环?(为什么不用将每个g[i][i]设为0?)
边权都是正值,不存在负环,所以不用处理
g[i][i]设为0,就相当于给i这个点加了一个权值为0的自环,这样就不符合规定了
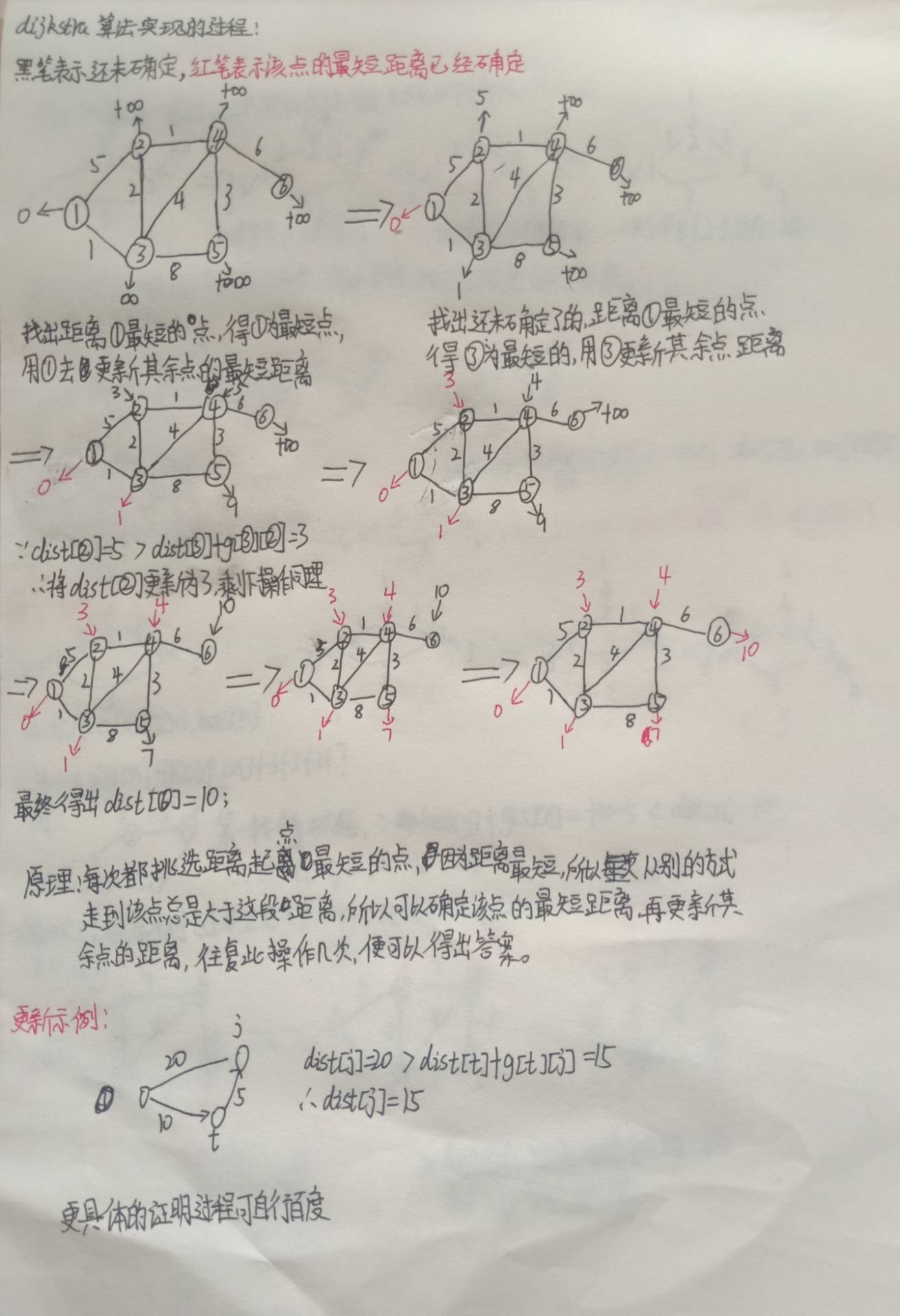
借图做个笔记
借个图
dist[ j ] = min(dist[ j ], dist[ t ] + g[ t ][ j ]);
//比较 起点到j的距离 和 起点到t的距离加上t到j的距离;
谢谢你的注释,解决了我的疑惑
大佬写的太棒了