题目描述

你正在经营一座摩天轮，该摩天轮共有 4 个座舱 ，每个座舱 最多可以容纳 4 位游客。你可以 逆时针 轮转座舱，但每次轮转都需要支付一定的运行成本 runningCost。摩天轮每次轮转都恰好转动 1 / 4 周。

给你一个长度为 n 的数组 customers，customers[i] 是在第 i 次轮转（下标从 0 开始）之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ，一旦该座舱再次抵达地面，他们就会离开座舱结束游玩。

你可以随时停下摩天轮，即便是 在服务所有游客之前。如果你决定停止运营摩天轮，为了保证所有游客安全着陆，将免费进行所有后续轮转。注意，如果有超过 4 位游客在等摩天轮，那么只有 4 位游客可以登上摩天轮，其余的需要等待 下一次轮转。

返回最大化利润所需执行的 最小轮转次数。 如果不存在利润为正的方案，则返回 -1。

样例

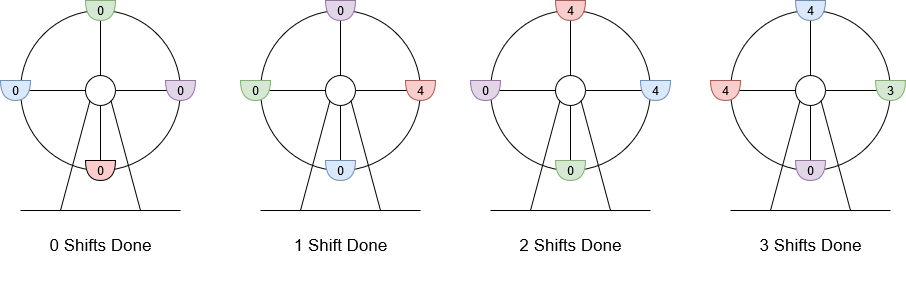
输入：customers = [8,3], boardingCost = 5, runningCost = 6
输出：3
解释：座舱上标注的数字是该座舱的当前游客数。
1. 8 位游客抵达，4 位登舱，4 位等待下一舱，摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14。
2. 3 位游客抵达，4 位在等待的游客登舱，其他 3 位等待，摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28。
3. 最后 3 位游客登舱，摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37。
轮转 3 次得到最大利润，最大利润为 $37。

输入：customers = [10,9,6], boardingCost = 6, runningCost = 4
输出：7
解释：
1. 10 位游客抵达，4 位登舱，6 位等待下一舱，摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20。
2. 9 位游客抵达，4 位登舱，11 位等待（2 位是先前就在等待的，9 位新加入等待的），摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40。
3. 最后 6 位游客抵达，4 位登舱，13 位等待，摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60。
4. 4 位登舱，9 位等待，摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80。
5. 4 位登舱，5 位等待，摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100。
6. 4 位登舱，1 位等待，摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120。
7. 1 位登舱，摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122。
轮转 7 次得到最大利润，最大利润为$122。

输入：customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出：-1
解释：
1. 3 位游客抵达，3 位登舱，0 位等待，摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89。
2. 4 位游客抵达，4 位登舱，0 位等待，摩天轮轮转。当前利润为 is 7 * $1 - 2 * $92 = -$177。
3. 0 位游客抵达，0 位登舱，0 位等待，摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269。
4. 5 位游客抵达，4 位登舱，1 位等待，摩天轮轮转。当前利润为 12 * $1 - 4 * $92 = -$356。
5. 1 位游客抵达，2 位登舱，0 位等待，摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447。
利润永不为正，所以返回 -1。

输入：customers = [10,10,6,4,7], boardingCost = 3, runningCost = 8
输出：9
解释：
1. 10 位游客抵达，4 位登舱，6 位等待，摩天轮轮转。当前利润为 4 * $3 - 1 * $8 = $4。
2. 10 位游客抵达，4 位登舱，12 位等待，摩天轮轮转。当前利润为 8 * $3 - 2 * $8 = $8。
3. 6 位游客抵达，4 位登舱，14 位等待，摩天轮轮转。当前利润为 12 * $3 - 3 * $8 = $12。
4. 4 位游客抵达，4 位登舱，14 位等待，摩天轮轮转。当前利润为 16 * $3 - 4 * $8 = $16。
5. 7 位游客抵达，4 位登舱，17 位等待，摩天轮轮转。当前利润为 20 * $3 - 5 * $8 = $20。
6. 4 位登舱，13 位等待，摩天轮轮转。当前利润为 24 * $3 - 6 * $8 = $24。
7. 4 位登舱，9 位等待，摩天轮轮转。当前利润为 28 * $3 - 7 * $8 = $28。
8. 4 位登舱，5 位等待，摩天轮轮转。当前利润为 32 * $3 - 8 * $8 = $32。
9. 4 位登舱，1 位等待，摩天轮轮转。当前利润为 36 * $3 - 9 * $8 = $36。
10. 1 位登舱，0 位等待，摩天轮轮转。当前利润为 37 * $3 - 10 * $8 = $31。
轮转 9 次得到最大利润，最大利润为 $36。

限制

• n == customers.length
• 1 <= n <= 10^5
• 0 <= customers[i] <= 50
• 1 <= boardingCost, runningCost <= 100

算法

(模拟) $O(n \cdot customers_i)$

1. 模拟整个过程，直到将所有人都送到摩天轮上。
2. 模拟的过程中，记录每次轮转后的利润，找到最大利润下的轮转次数。

时间复杂度

• 最多有 $n \cdot customers_i$ 位游客，每次轮转至少带走一位乘客，故总时间复杂度为 $O(n \cdot customers_i)$。

空间复杂度

• 仅需要常数的额外空间。

Go 代码

func minOperationsMaxProfit(customers []int, boardingCost int, runningCost int) int {
    var totCostomers, profit, currentRound int
    n := len(customers)
    maxProfit := -1000000000;
    roundForMaxProfit := -1;
    for currentRound < n || totCostomers > 0 {
        if currentRound < n {
            totCostomers += customers[currentRound]
        }
        if totCostomers >= 4 {
            profit += boardingCost * 4 - runningCost
            totCostomers -= 4;
        } else {
            profit += boardingCost * totCostomers - runningCost
            totCostomers = 0;
        }

        if maxProfit < profit {
            maxProfit = profit
            roundForMaxProfit = currentRound
        }
        currentRound++
    }

    if maxProfit <= 0 {
        return -1
    }
    return roundForMaxProfit + 1
}