题目描述

我们有 n 栋楼，编号从 0 到 n - 1。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests，其中 requests[i] = [from_i, to_i]，表示一个员工请求从编号为 from_i 的楼搬到编号为 to_i 的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0，一个员工要离开楼 1，一个员工要离开楼 2，如果该请求列表可行，应该要有两个员工搬入楼 0，一个员工搬入楼 1，一个员工搬入楼 2。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

样例

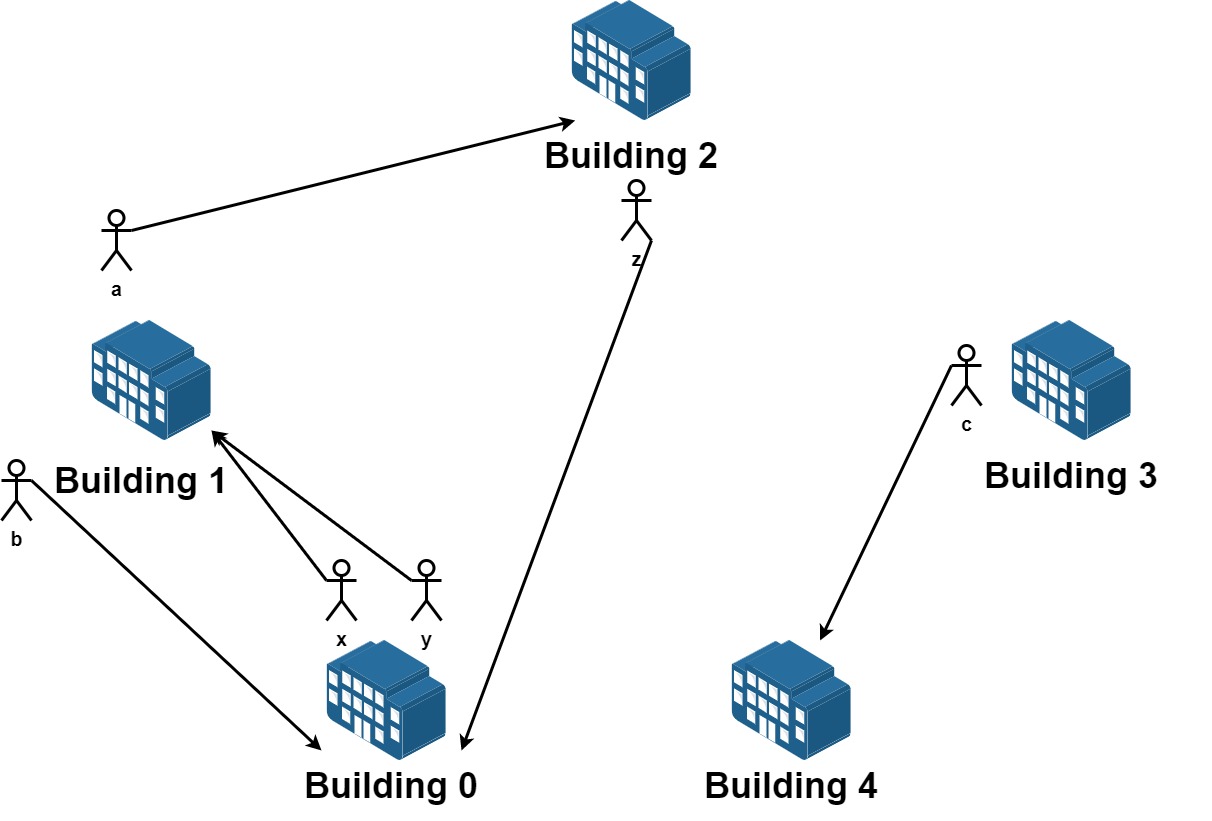
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

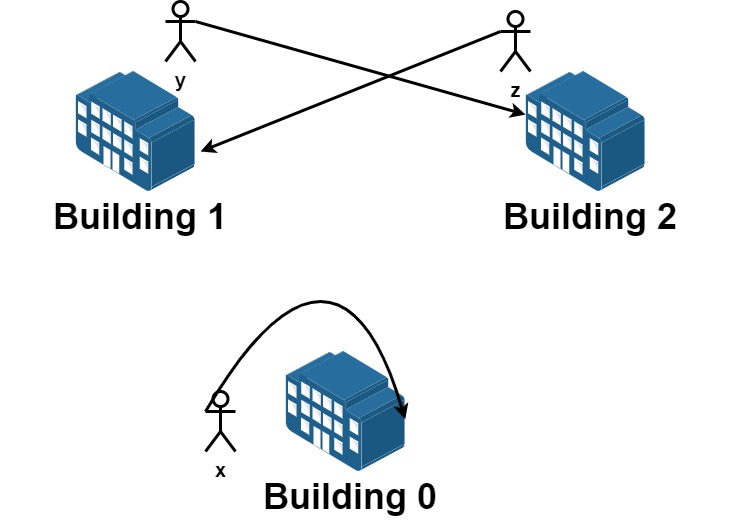
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

输入：n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出：4

限制

• 1 <= n <= 20
• 1 <= requests.length <= 16
• requests[i].length == 2
• 0 <= from_i, to_i < n

算法

(递归回溯) $O(n2^m)$

1. 递归遍历每种请求的组合，找到合法的组合，记录下其最大的请求数目。

时间复杂度

• 共有 $O(2^m)$ 种组合，每种需要 $O(n)$ 的时间验证，故总时间复杂度为 $O(n2^m)$。其中 $m$ 为总的请求数。

空间复杂度

• 需要 $O(n + m)$ 的额外空间记录每栋楼的增减人数和系统栈。

C++ 代码

class Solution {
private:
    bool check(const vector<int> &buildings) {
        for (int b : buildings)
            if (b != 0)
                return false;
        return true;
    }

    void solve(int i, int m, const vector<vector<int>> &requests,
               int selected, int &ans, vector<int> &buildings) {
        if (i == m) {
            if (check(buildings))
                ans = max(ans, selected);
            return;
        }

        solve(i + 1, m, requests, selected, ans, buildings);

        buildings[requests[i][0]]--;
        buildings[requests[i][1]]++;
        solve(i + 1, m, requests, selected + 1, ans, buildings);
        buildings[requests[i][0]]++;
        buildings[requests[i][1]]--;
    }

public:
    int maximumRequests(int n, vector<vector<int>>& requests) {
        int ans = 0;
        vector<int> buildings(n, 0);
        solve(0, requests.size(), requests, 0, ans, buildings);
        return ans;
    }
};