题目

原题链接

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

实现思路

当然可以暴力计算，但是会超时。

此题的主要思路是构建一个差分矩阵，然后进行计算。
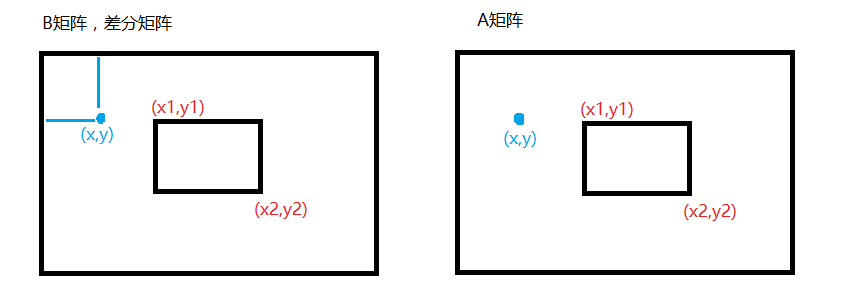
什么是差分矩阵？如下图，B矩阵就是A矩阵的差分矩阵。A矩阵（x,y）处的值等于B矩阵（x,y）处的值及其左上角所有元素的值相加。

1. 首先，如下图，假设我们已经有了一个差分矩阵B和原矩阵A，如果A矩阵的(x1,y1)到(x2,y2)这片区域都增加一个c值，那对应的B矩阵中：

   B[x1,y1]+=c;
   B[x1,y2+1]+=c;
   B[x2+1,y1]+=c;
   B[x2+1,y2+1]-=c;

1. 看懂上面的过程后，就可以通过上面的思路由A矩阵构建B矩阵了，可以想象A矩阵和B矩阵刚开始全是0，然后在A矩阵的(x,y)处输入一个值，相当于在A矩阵的(x,y)处的值增加一个c，这个时候就根据步骤1里面的思路更新B矩阵，一直循环到A矩阵全部由0增长为输入的矩阵，B矩阵就构建完毕。

A(x,y)处的值由0增加到A[x,y]:

B[x,y]+=A[x,y];
B[x,y+1]+=A[x,y];
B[x+1,y]+=A[x,y];
B[x+1,y+1]-=A[x,y];

1. 由B差分矩阵构建新的A矩阵。
   既然B是A矩阵的差分矩阵，那:

   A[i][j] = A[i - 1][j] + A[i][j - 1] - A[i - 1][j - 1] + B[i][j];

代码实现

#include <iostream>
#include <vector>

using namespace std;


int main()
{
    int n, m, q;
    cin >> n >> m >> q;

    vector<vector<int>> D(n+1, vector<int>(m+1, 0));
    for (int i = 1; i < n+1; i++)
        for (int j = 1; j < m+1; j++)
            cin >> D[i][j];

    //计算差分矩阵
    vector<vector<int>> V(n + 2, vector<int>(m + 2, 0));//+2是为了保证不溢出

    for(int i = 1;i<n+1;i++)
        for (int j = 1; j < m + 1; j++)
        {
            V[i][j] += D[i][j];
            V[i+1][j] -= D[i][j];
            V[i][j+1] -= D[i][j];
            V[i+1][j+1] += D[i][j];
        }

    //输入x1,y1,x2,y2

    int x1, x2, y1, y2,c;
    while (q--)
    {
        cin >> x1 >> y1>>x2 >> y2 >> c;

        V[x1][y1] += c;
        V[x2 + 1][y1] -= c;
        V[x1][y2 + 1] -= c;
        V[x2+1][y2+1] += c;
    }

    //输出
    for (int i = 1; i < n + 1; i++)
    {
        for (int j = 1; j < m + 1; j++)
        {
            D[i][j] = D[i - 1][j] + D[i][j - 1] - D[i - 1][j - 1] + V[i][j];
            cout << D[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}