n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

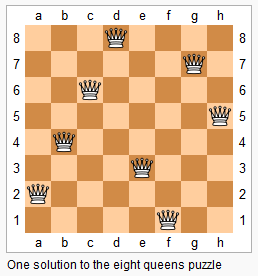
现在给定整数n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数n。

输出格式

每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。

其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
…Q
Q…
..Q.

..Q.
Q…
…Q
.Q..

Go 代码

第一种搜索顺序，按行枚举，每行枚举一个

package main

import "fmt"

var n int
var g [][]string
var col []bool // 标记是否写过了
var dg []bool  // 正对角线
var udg []bool // 反对角线

func main() {
    fmt.Scan(&n)
    g = make([][]string, n)
    for i := 0; i < len(g); i++ {
        g[i] = make([]string, n)
    }
    col = make([]bool, 2*n)
    dg = make([]bool, 2*n)
    udg = make([]bool, 2*n)

    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            g[i][j] = "." // 初始化
        }
    }
    dfs(0)
}

func dfs(u int) {
    if u == n { // 找到一组方案
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                fmt.Print(g[i][j])
            }
            fmt.Println()
        }
        fmt.Println()
    }
    for i := 0; i < n; i++ {
        // 这一列之前没有放过 && 对角线上没有放过 && 反对角线也没有放过
        if !col[i] && !dg[u+i] && !udg[n-u+i] {
            g[u][i] = "Q"                                     // 选定该位置为 皇后
            col[i], dg[u+i], udg[n-u+i] = true, true, true    // 这一行这一条对角线和反对角线都不能有皇后了
            dfs(u + 1)                                        // 
            col[i], dg[u+i], udg[n-u+i] = false, false, false // 恢复现场
            g[u][i] = "."
        }
    }
}

Go 代码 第二种搜索顺序

package main

import "fmt"

var n int
var g [][]string
var row []bool
var col []bool // 标记是否写过了
var dg []bool  // 正对角线
var udg []bool // 反对角线

func main() {
    fmt.Scan(&n)
    g = make([][]string, n)
    for i := 0; i < len(g); i++ {
        g[i] = make([]string, n)
    }
    row = make([]bool, 2*n)
    col = make([]bool, 2*n)
    dg = make([]bool, 2*n)
    udg = make([]bool, 2*n)

    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            g[i][j] = "." // 初始化
        }
    }
    dfs(0, 0, 0) // 从左上角开始搜索，并记录当前有多少个皇后
}

func dfs(x, y, s int) {
    if y == n { // 该行出界则转移到下一行
        y, x = 0, x+1 // 枚举下一行
    }
    if x == n { // 枚举完最后一行
        if s == n { // 如果当前摆的皇后等于 n
            for i := 0; i < n; i++ { // 输出符合的解
                for j := 0; j < n; j++ {
                    fmt.Print(g[i][j])
                }
                fmt.Println()
            }
            fmt.Println()
        }
        return 
    }

    // 不放皇后
    dfs(x, y+1, s) // 移动到该行的下一个格子

    // 放皇后,这一行没有皇后&&这一列没有皇后&&正对角线没有皇后&&反对角线没有皇后
    if !row[x] && !col[y] && !dg[x+y] && !udg[x-y+n] {
        g[x][y] = "Q"
        row[x], col[y], dg[x+y], udg[x-y+n] = true, true, true, true
        dfs(x, y+1, s+1)
        row[x], col[y], dg[x+y], udg[x-y+n] = false, false, false, false
        g[x][y] = "."
    }
}

Go 代码的 简洁版本

来自 acwa

package main

import "fmt"

var n int
var path []int
var st []bool // 标记是否写过了
var ln []int

func dfs(u int){
    if u == n{
        for i:=0; i<n; i++{
            for j:=1; j<=n; j++{
                if path[i]==j{
                    fmt.Printf("Q")
                } else {
                    fmt.Printf(".")
                }
            }
            fmt.Println()
        }
        fmt.Println()
    }
    for i:=1; i<=n; i++{
        if st[i] == false{
            ln[u+1] = i - u - 1
            flag := true
            for j:=u; j>=1; j--{
                if ln[u+1] == ln[j] || ((u+1 + i)== (j + path[j-1])){
                    flag = false
                    break
                }
            }
            if flag {
                path[u] = i // 不用恢复，因为path本来就是被覆盖的
                st[i] = true
                dfs(u+1)
                st[i] = false // 一定要恢复现场，因为有判定取决于st的值
            }
        }
    }
}

func main(){
    _, _ = fmt.Scanf("%d", &n)
    path = make([]int, n)
    st = make([]bool, n+1)
    ln = make([]int, n+1)
    dfs(0)
}

作者：acwa
链接：https://www.acwing.com/activity/content/code/content/216298/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。