题目描述

Yura is tasked to build a closed fence in shape of an arbitrary non-degenerate simple quadrilateral. He’s already got three straight fence segments with known lengths a, b, and c. Now he needs to find out some possible integer length d of the fourth straight fence segment so that he can build the fence using these four segments. In other words, the fence should have a quadrilateral shape with side lengths equal to a, b, c, and d. Help Yura, find any possible length of the fourth side.

A non-degenerate simple quadrilateral is such a quadrilateral that no three of its corners lie on the same line, and it does not cross itself.

Input
The first line contains a single integer t — the number of test cases (1≤t≤1000). The next t lines describe the test cases.

Each line contains three integers a, b, and c — the lengths of the three fence segments (1≤a,b,c≤109).

Output
For each test case print a single integer d — the length of the fourth fence segment that is suitable for building the fence. If there are multiple answers, print any. We can show that an answer always exists.
Note
We can build a quadrilateral with sides 1, 2, 3, 4.

We can build a quadrilateral with sides 12, 34, 56, 42.

样例

2
1 2 3
12 34 56

4
42

此题题意 给你a b c 三条边 让你求出第四条边 使得这个四条边可以构成一个四边形
解法一
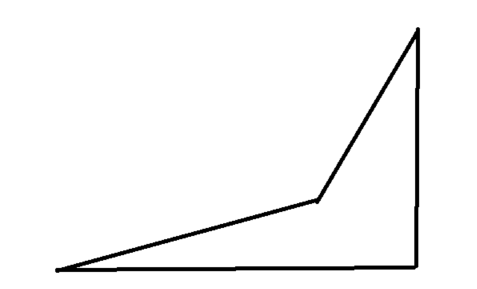
我们可以找出3条边中最大的那一条 让第四条边的长度与其相等 构成四边形的形状是这样的

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin>>t;
    while(t--)
    {
        int ans=-1;
        for(int i=1;i<=3;i++)
        {
            int x;
            cin>>x;
            ans=max(x,ans);
        }
        cout<<ans<<endl;
    }
    return 0;
 } 

解法二
因为考虑到不交叉情况 其实只要构成四边形就不会有交叉情况 满足 d<a+b+c 又因为d是整数所以需要输出a+b+c-1即可

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin>>t;
    while(t--)
    {
        long long a,b,c;
        cin>>a>>b>>c;
        cout<<a+b+c-1<<endl;
    }
    return 0;
 } 

解法三
是我们求出d的最大范围和最小范围 然后从中随便s选一个数输出

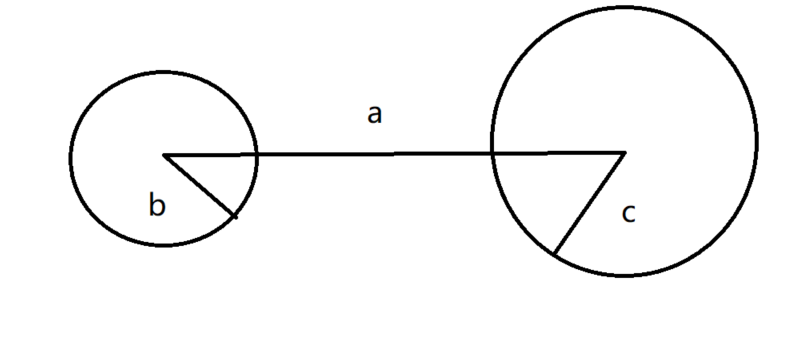
咱们假设 a是给定3条边中最大的边 以a俩端点为圆心 b c长度为半径构建一个园 d的范围就是 a-b-c<d<a+b+c
首先咱们看右边 d<a+b+c 如果d=a+b+c a,b,c,d是构不成一个四边形的 因为都在同一条直线上 让d小于a+b+c 就可以构成
一个四边形
然后咱们看左边 a-b-c<d 这是d的最小取值 也是不可以取到a-b-c 如果取到那就重合了不能构成四边形
如果 a 不是 最大的边 那就相当于 俩个圆出现了相交的情况

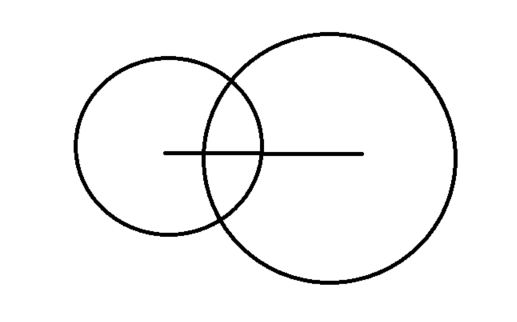
这时候 a-b-c是小于0的 又因为d 是大于0的整数 所以1<=d<a+b+c
代码中要注意 找出的值是最大值 如何用最大值和3条边之和来凑出 最大值减去另外2条边
咱们这里假设 a是最大值 a-b-c=a-(a+b+c)+a
咱们就可以得出 d的最小范围是 2*max(a,max(b,c))-(a+b+c)

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin>>t;
    while(t--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        int maxii=max(a,max(b,c));
        int ans=2*maxii-(a+b+c);
        if(ans<0) ans=1;
        else ans++;
        cout<<ans<<endl;
    }
    return 0;
}