AcWing 252. 树

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 252. 树原题链接困难

作者：

Wizard , 2020-10-07 10:51:20 , 所有人可见 , 阅读 967

这是一道点分治的模板题

~~下文输入格式略有不同别说我没提醒你~~

题目描述

给定一个有 $N$ 个点（编号 $1,2,…,N$）的树，每条边都有一个权值（不超过 $1000$）。
树上两个节点x与y之间的路径长度就是路径上各条边的权值之和。
求长度不超过K的路径有多少条。

输入格式

输入包含多组测试样例。
每组测试样例的第一行包含两个正整数 $N$ 和 $K$。
接下来 $N-1$ 行，每行包含三个正整数 $u,v,l$，表示节点 $u$ 与 $v$ 之间存在一条边，且边的权值为 $l$。
当输入样例 $N=0,K=0$ 时，表示输入终止，且该样例无需处理。

输出格式

每个测试样例输出一个结果。
每个结果占一行。

Sample Input / Output

进入正文

首先对于这道题一个很暴力的想法：枚举每个点对看看之间的距离是否 $ \le k$，复杂度应该是 $O(n^2logn)\ ?\ $反正绝对过不了。

首先我们来分析一下，树上两点之间的路径有一下两种情况
+ 1. 经过根节点
+ 2. 不经过根节点（即两个点在当前根节点的同一子树内）

对于情况一：
$dis(u,v)=dis(u,root)+dis(root,v)$
对于情况二：
我们可以找到 $u,v$ 路径所在的子树，将根节点变为子树的根节点，然后就变为了第一种情况，即我们可以不断的递归到子树的根节点，将所有情况转化为第一种情况求出答案

不难发现，这样递归下去的 复杂度和树的深度有关，所以我们应尽量的减小树的深度以优化复杂度，那么我们怎么办呢？
对于每一棵树，我们都有一个重心，其所有的子树中最大的子树节点数最少，也就是说删去重心后生成的多棵树会尽可能平衡。
拿输入样例举个例子，假如树长这样，最大深度为 $4$，极其不优秀：

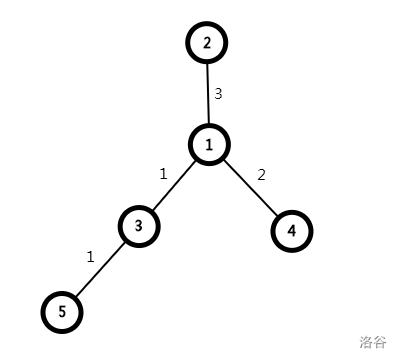
但是这样就优美的多了：最大深度为 $3$，我们称此时的根节点为“树的重心”

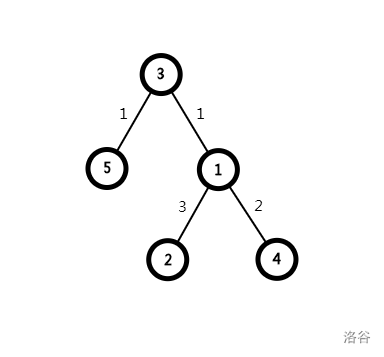
求树的重心也不难，一路扫下去就完事了：$O(n)$
$code:$

int maxx,root,smax[N],size[N];
//maxx=smax[root],root为树的重心
//smax[i]表示i的最大子树的大小
//size[i]表示以i为跟的子树大小 
void dfs(int x,int fa)
{
    smax[x]=0;size[x]=1;
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;if(y==fa) continue;
        dfs(y,x);size[x]+=size[y];
        smax[x]=mymax(smax[x],size[y]);
    }
    smax[x]=mymax(smax[x],n-size[x]);
    maxx=mymin(maxx,smax[x]);
    root=(maxx==smax[x])?x:root;
}

那么如何计算点对方案数呢？ 当然是求出每个节点到树的重心的距离（记为 $dis[i]$），枚举点对 $(i,j)\ \ \ $ $if(dis[i]+dis[j]\le k)\ \ ans++$，这里有一个优化，可以把 $dis$ 数组排个序，用 $l,r$ 两个指针分别从前、后扫描 $dis$ 数组，显然随着 $l$ 从左到右扫，$r$ 是从右到左单调递减的，代码如下：

for(int l=1,r=dis[0];l<r;)//尝试把两条根节点到子节点（包括根节点）的路径合并成一条经过根节点的路径 
{
    if(dis[l]+dis[r]<=k) sum+=r-l/*dis[l]+dis[l+1~r-1]<=k*/,l++;
    else r--;
}

不过，枚举的点对 $(i,j)$ 间的路径可能属于上文提到的情况二，逛了一圈题解，发现很多是容斥修正的：

int calc(int x,int dst)//计算以x为根的所有情况的答案
{
    get_dis(x,dis[0]=0,dst);
    sort(dis+1,dis+dis[0]+1);
    int sum=0;
    for(int l=1,r=dis[0];l<r;)//尝试把两条根节点到子节点（包括根节点）的路径合并成一条经过根节点的路径 
    {
        if(dis[l]+dis[r]<=k) sum+=r-l/*dis[l]+dis[l+1~r-1]<=k*/,l++;
        else r--;
    }
    return sum;
}
void solve(int x)//求解以x为重心的情况
{
    vis[x]=true;
    ans+=calc(x,0);
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(vis[y]) continue;
        ans-=calc(y,a[k].d);//减去不合法的情况 
        maxx=point=size[y];
        get_root(y,x);solve(root);
    }
}

当然也有不用容斥原理修正答案的，我就拱一篇题解上来。

只需要让这棵子树和前面的子树拼，即可避免两个点都在一棵子树中的情况，不过对于 dis 数组的排序要稍微注意，具体看注释：（只有 calc 函数不同）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e4+10;
inline int mymin(int a,int b) {return a<b?a:b;}
inline int mymax(int a,int b) {return a>b?a:b;}
inline int read()
{
    int x=0;bool f=false;
    char ch=getchar();
    while(ch<'0' || ch>'9') f|=(ch=='-'),ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
    return f?-x:x;
}
int n,k,ans,point;//point为点数 
struct node{int y,d,next;}a[N<<1];int len,last[N];
inline void ins(int x,int y,int d) {a[++len].y=y;a[len].d=d;a[len].next=last[x];last[x]=len;}
/*找到一个点，其所有的子树中最大的子树节点数最少，
那么这个点就是这棵树的重心，删去重心后，生成的多棵树尽可能平衡。*/
int maxx,root,size[N],smax[N];//size->以己为跟的子树大小  smax->最大子树的大小
bool vis[N];//求重心时避免重复访问
void get_root(int x,int fa)
{
    siz[x]=1;smax[x]=0;
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(y==fa || vis[y]) continue;
        get_root(y,x);
        siz[x]+=siz[y];
        smax[x]=mymax(smax[x],siz[y]);
    }
    smax[x]=mymax(smax[x],point-siz[x]);
    minn=mymin(minn,smax[x]);
    root=minn==smax[x]?x:root;
}
int num,dis[N];
void dfs(int x,int fa,int Dis)
{
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(y==fa || vis[y]) continue;
        dis[++num]=Dis+a[k].d;
        dfs(y,x,Dis+a[k].d);
    }
}
int dd[N];
int calc(int x)//计算以x为根的所有情况的答案
{
    int ret=0;
    dis[num=1]=0;
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(vis[y]) continue;
        dis[++num]=a[k].d;
        int st=num;
        dfs(y,x,a[k].d);
        sort(dis+st,dis+num+1);//对这棵子树进行排序，不要和之前的打乱成一坨了
        for(int l=1,r=num;l<st && r>=st;)
        {
            if(dis[l]+dis[r]<=limit) ret+=r-st+1,l++;
            else r--;
        }
        int len=0,i=1,j=st;//因为前面子树的 dis 已经有序，所以直接归并起来即可，用 sort 会 T ！！！
        while(i<st || j<=num)
        {
            if(j>num || (i<st && dis[i]<=dis[j])) dd[++len]=dis[i++];
            else dd[++len]=dis[j++];
        }
        memcpy(dis,dd,sizeof(dis));
    }
    return ret;
}
int ans;
void solve(int x)//求解以x为重心的情况
{
    vis[x]=true;
    ans+=calc(x);
    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(vis[y]) continue;
        minn=point=siz[y];
        get_root(y,x);
        solve(root);
    }
}
void clear()
{
    len=0;memset(last,0,sizeof(last));
    memset(vis,false,sizeof(vis));ans=0;
}
int main()
{
    n=read();limit=read();
    while(n || limit)
    {
        clear();
        for(int i=1;i<n;i++)
        {
            int x=read(),y=read(),d=read();
            ins(x,y,d);ins(y,x,d);
        }
        minn=point=n;
        get_root(1,0);
        solve(root);
        printf("%d\n",ans);
        n=read();limit=read();
    }
    return 0;
}