题目描述

你有 k 个服务器，编号为 0 到 k-1，它们可以同时处理多个请求组。每个服务器有无穷的计算能力但是 不能同时处理超过一个请求。请求分配到服务器的规则如下：

• 第 i（序号从 0 开始）个请求到达。
• 如果所有服务器都已被占据，那么该请求被舍弃（完全不处理）。
• 如果第 (i % k) 个服务器空闲，那么对应服务器会处理该请求。
• 否则，将请求安排给下一个空闲的服务器（服务器构成一个环，必要的话可能从第 0 个服务器开始继续找下一个空闲的服务器）。比方说，如果第 i 个服务器在忙，那么会查看第 (i+1) 个服务器，第 (i+2) 个服务器等等。

给定一个 严格递增 的正整数数组 arrival，表示第 i 个任务的到达时间，和另一个数组 load，其中 load[i] 表示第 i 个请求的工作量（也就是服务器完成它所需要的时间）。你的任务是找到 最繁忙的服务器。最繁忙定义为一个服务器处理的请求数是所有服务器里最多的。

请你返回包含所有 最繁忙服务器 序号的列表，你可以以任意顺序返回这个列表。

样例

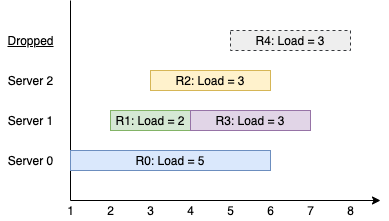
输入：k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3] 
输出：[1] 
解释：
所有服务器一开始都是空闲的。
前 3 个请求分别由前 3 台服务器依次处理。
请求 3 进来的时候，服务器 0 被占据，所以它被安排到下一台空闲的服务器，也就是服务器 1 。
请求 4 进来的时候，由于所有服务器都被占据，该请求被舍弃。
服务器 0 和 2 分别都处理了一个请求，服务器 1 处理了两个请求。所以服务器 1 是最忙的服务器。

输入：k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
输出：[0]
解释：
前 3 个请求分别被前 3 个服务器处理。
请求 3 进来，由于服务器 0 空闲，它被服务器 0 处理。
服务器 0 处理了两个请求，服务器 1 和 2 分别处理了一个请求。所以服务器 0 是最忙的服务器。

输入：k = 3, arrival = [1,2,3], load = [10,12,11]
输出：[0,1,2]
解释：每个服务器分别处理了一个请求，所以它们都是最忙的服务器。

输入：k = 3, arrival = [1,2,3,4,8,9,10], load = [5,2,10,3,1,2,2]
输出：[1]

输入：k = 1, arrival = [1], load = [1]
输出：[0]

限制

• 1 <= k <= 10^5
• 1 <= arrival.length, load.length <= 10^5
• arrival.length == load.length
• 1 <= arrival[i], load[i] <= 10^9
• arrival 保证 严格递增。

算法

(有序集) $O(n \log n + k)$

1. 建立一个集合，存储当前所有待处理的请求，且按照开始时间从小到大排序。
2. 用一个数组记录当前每台服务器上个任务的结束时间。
3. 遍历每个请求，首先将该请求加入到待处理请求的集合中。对于 i % k 的服务器来说，不断地从待处理请求的集合中挑选出可以执行的，且开始时间最小的请求，这一步可以通过集合的二分操作 (lower_bound) 来实现。
4. 如果取出的请求已经超过了 k 轮，则说明当初加入该请求时，不存在空闲的服务器，直接丢弃。用取出的请求来更新当前服务器的结束时间。
5. 扫描所有服务器，统计答案。

时间复杂度

• 每个请求进出集合一次，每次进出需要 $O(\log n)$ 的时间。
• 寻找答案需要 $O(k)$ 的时间，故总时间复杂度为 $O(n \log n + k)$。

空间复杂度

• 需要 $O(n + k)$ 的额外空间存储每台服务器的结束时间，维护集合和答案。

C++ 代码

struct Request {
    int st, ed, idx;
    Request(int st_, int ed_, int idx_):st(st_), ed(ed_), idx(idx_){}
    bool operator < (const Request &another) const {
        return st < another.st;
    }
};

class Solution {
public:
    vector<int> busiestServers(int k, vector<int>& arrival, vector<int>& load) {
        const int n = arrival.size();
        vector<int> finishingTime(k, 0), res(k, 0);
        set<Request> pendingRequests;
        for (int i = 0; i < n + k; i++) {
            int j = i % k;
            if (i < n)
                pendingRequests.insert(Request(arrival[i], arrival[i] + load[i], i));
            while (1) {
                auto it = pendingRequests.lower_bound(Request(finishingTime[j], -1, -1));
                if (it == pendingRequests.end())
                    break;
                if (i - it->idx < k) {
                    res[j]++;
                    finishingTime[j] = it->ed;
                }
                pendingRequests.erase(it);
            }
        }

        int maxNum = 0;
        for (int i = 0; i < k; i++)
            if (maxNum < res[i])
                maxNum = res[i];

        vector<int> ans;
        for (int i = 0; i < k; i++)
            if (maxNum == res[i])
                ans.push_back(i);

        return ans;
    }
};