分析：

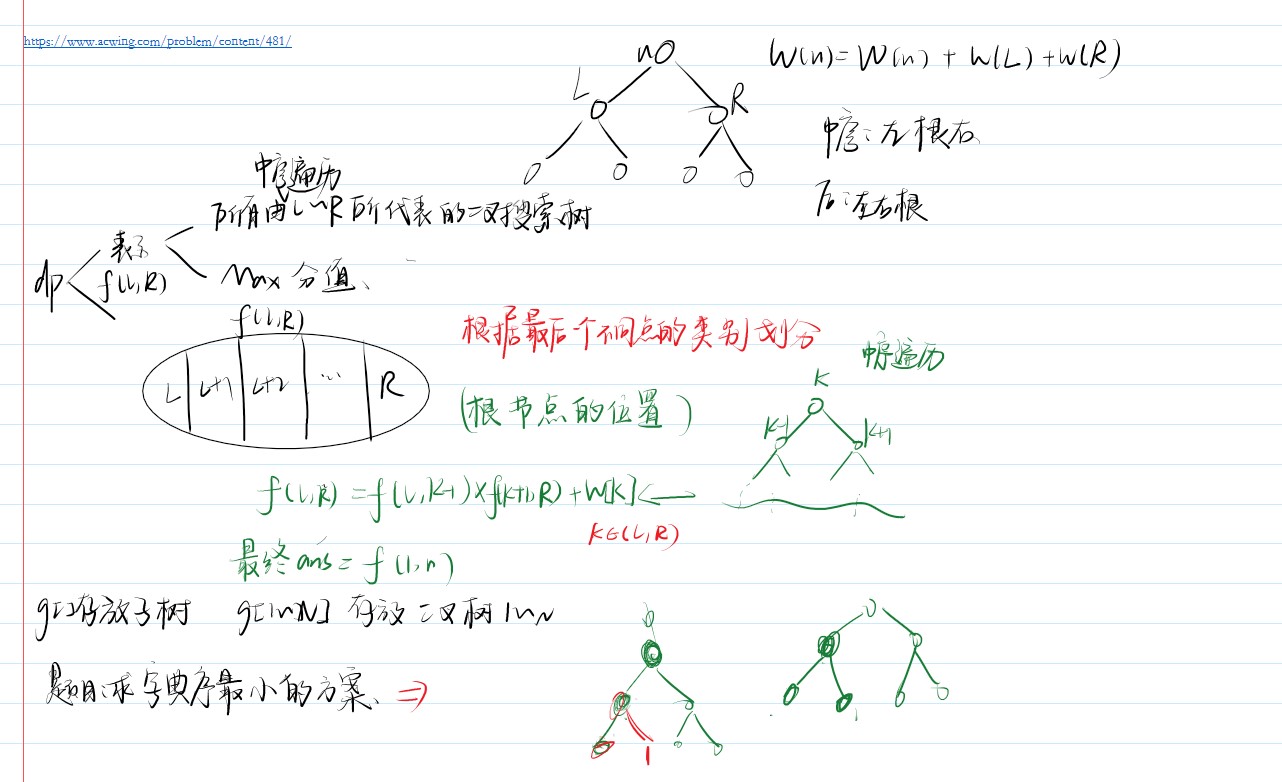
循环方式

#include<iostream>
#include<cstring>
using namespace std;
const int N = 31;
int f[N][N], w[N], g[N][N];

void dfs(int l, int r)
{
    if(l > r)return ;
    int root = g[l][r];
    cout << root << " ";
    dfs(l, root - 1);
    dfs(root + 1, r);
}


int main()
{
    int n; cin >> n; 
    for(int i = 1; i <= n; ++i)
    {
        cin >> w[i];
    }
    for(int i = 1; i <= n; ++i)
    {
        f[i][i] = w[i];
        g[i][i] = i;
    }
    for(int len = 1; len < n; ++ len)
        for(int l = 1; l + len <= n; ++ l)
        {
            int r = l + len;
            for(int k = l; k <= r; ++k)
            {
                int left = k == l ? 1 : f[l][k - 1];
                int right = k == r ? 1 : f[k + 1][r];
                int s =  left * right + w[k];
                if(s > f[l][r])
                {
                    f[l][r] = s;
                    g[l][r] = k;
                }
            }
        }
    cout << f[1][n] <<endl;
    dfs(1, n);
    return 0;
}

记忆化深搜

#include<iostream>
#include<cstring>
#define x first
#define y second
using namespace std;
const int N = 31;
int f[N][N], w[N], g[N][N];

void dfs(int l, int r)
{
    if(l > r)return ;
    int root = g[l][r];

    cout << root << " ";
    dfs(l, root - 1);
    dfs(root + 1, r);
}

pair<int , int> dp(int l, int r)
{
    int val = 0;
    if(f[l][r] > 0)return {f[l][r], g[l][r]};
    if(l >= r)
    {
        g[l][l] = l;
        return {w[l], g[l][l]};
    }
    for(int i = l; i <= r; ++i)
    {
        if(i == l)val = dp(i + 1, r).x + w[i];
        else if(i == r)val = dp(l , i - 1).x + w[i];
        else val = dp(l, i - 1).x * dp(i + 1, r).x + w[i];
        if(f[l][r] < val)
        {
            f[l][r] = val;
            g[l][r] = i;
        }
       // cout << l << ' ' <<r << ' ' << g[l][r] << endl;
    }
    return {f[l][r], g[l][r]};
}

int main()
{
    memset(f, -1, sizeof f);
    int n; cin >> n; 
    for(int i = 1; i <= n; ++i)
    {
        cin >> w[i];
    }
    cout << dp(1, n).x <<endl;
    dfs(1, n);
    return 0;
}