本题将学到：

1、dfs求树的直径：(树中最长的一条边),时间复杂度$O(n)$
    算法：
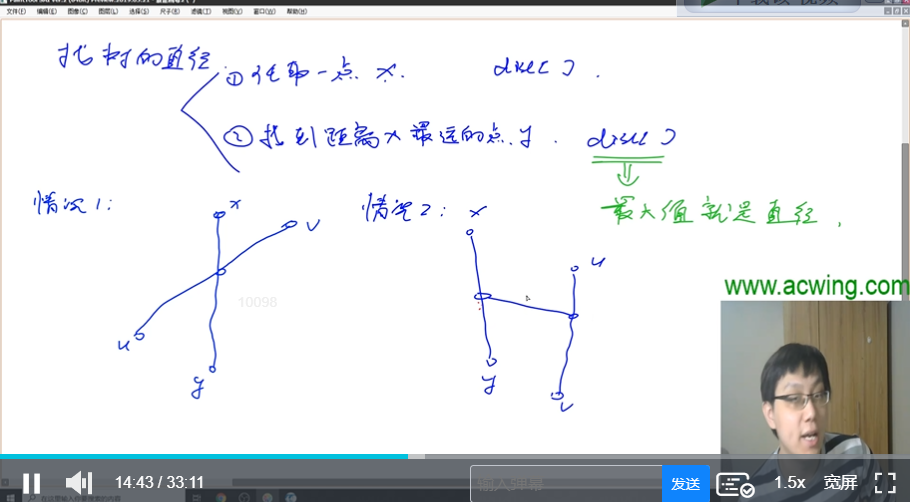
        1. 任选一点x，求出dist[]
        2. 找到距离x最远的点y【必然是直径的端点】，再求一遍dist[],其中最大值就是直径【直径的另一个端点】
    证明参考y总视频

2、图的存储：用vector实现邻接表

证明：

设 |uv|是一条直径，y是x的最远点
情况1： 相交。有 |yu| >= |uv|, 所以|yu|也是一条直径
情况2：不相交。也有 |yu| >= |uv|, 所以|yu|也是一条直径

综上，|yu| 是一条直径。【其中y是x的最远点，u是y的最远点，求两边dfs，O(n)】

#include <iostream>
#include <vector>

using namespace std;

const int N = 100010;

int n;
struct Node{
    int id,w;
};
vector<Node> h[N];
int dist[N];

void dfs(int u,int father,int distance)
{
    dist[u] = distance;

    for(auto node : h[u])
        if(node.id != father)
            dfs(node.id, u, distance + node.w);
}

int main()
{
    cin >> n;
    for(int i = 0;i < n - 1;i ++)
    {
        int a,b,w;
        cin >> a >> b >> w;
        h[a].push_back({b,w}); // 无向图建双向边
        h[b].push_back({a,w});
    }

    dfs(1,-1,0);

    int u = 1;
    for(int i = 1;i <= n; i++ )
        if(dist[i] > dist[u])
            u = i;

    dfs(u,-1,0);

    for(int i = 1;i <= n; i++ )
        if(dist[i] > dist[u])
            u = i;

    int s = dist[u]; // s就是树的直径
    printf("%lld\n",s * 10 + s * (s + 1ll) / 2); // 注意最坏情况下爆int

    return 0;
}