题目描述

假设我们有一个用下图表示的文件系统：

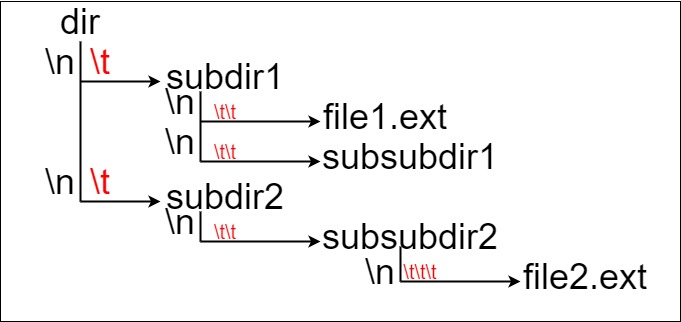
我们用字符串来表示一个文件系统，其中 \n\t 是主目录的一个子目录，\n\t\t 是主目录的子目录下的一个子目录，依次类推。每个文件夹都被表示为一个由字母 和（或） 数字组成的字符串。每个文件都是以 s1.s2 的形式表示，且 s1 和 s2 都是由字母 和（或） 数字组成的字符串。

例如，上图的文件系统可被表示为 "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"。

给定一个字符串表示按上述规则形成的文件系统，返回文件系统中绝对路径最长的 文件。如果没有任何文件，返回 0。

样例

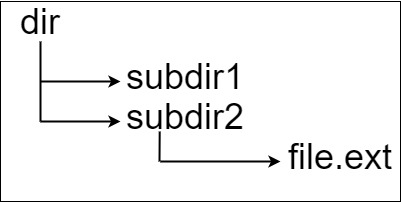
输入：input = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext"
输出：20
解释：我们仅有一个文件且它的路径为 "dir/subdir2/file.ext"，长度是 20。
路径 "dir/subdir1" 不包含任何文件。

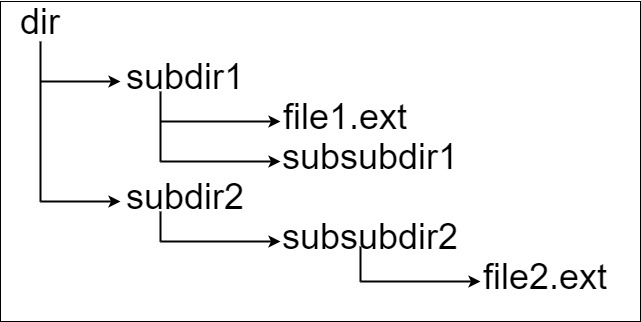
输入：input = "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"
输出：32
解释：我们有两个文件：
"dir/subdir1/file1.ext" 长度为 21，
"dir/subdir2/subsubdir2/file2.ext" 长度为 32。
我们返回 32 因为它有最长的路径。

输入：input = "a"
输出：0
解释：文件系统中没有任何文件。

限制

• 1 <= input.length <= 10^4
• 输入可能包含小写英文字母，大写英文字母，换行符 '\n'，缩进符 '\t'，点 '.'，空格 ' '，和数字。

算法

(字符串处理，栈) $O(n)$

1. 设计两个栈，一个存储每个名字的长度，一个存储当前名字对应的 level。根目录的 level 为 0。维护一个记录当前路径长度的变量 length。
2. 每次获取下一个目录（文件）的 level 和名字。如果栈顶的 level 大于等于当前目录（文件）的 level，则栈顶不断出栈，且 length 减去当前 level 名字的长度。
3. 然后将当前目录（文件）进栈，更新 length。如果当前名字是个文件，则用 length + level 更新答案。

时间复杂度

• 每个名字仅被遍历常数次，且最多进栈一次，出栈一次，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储名字长度和对应 level 的栈。

C++ 代码

class Solution {
private:
    bool isFile(const string &name) {
        const int len = name.size();
        for (int i = len - 1; i >= 0; i--)
            if (name[i] == '.' && i != len - 1)
                return true;

        return false;
    }

    int getNextLevel(int &i, const string &input) {
        int res = 0;
        while (i < input.size() && (input[i] == '\t' || input[i] == '\n')) {
            if (input[i] == '\t')
                res++;
            i++;
        }
        return res;
    }

    string getNextName(int &i, const string &input) {
        string name;
        while (i < input.size() && input[i] != '\n') {
            name.push_back(input[i]);
            i++;
        }
        return name;
    }

public:
    int lengthLongestPath(string input) {
        stack<int> lengthStack, levelStack;
        int length = 0, maxLength = 0;
        int i = 0;
        while (i < input.size()) {
            int level = getNextLevel(i, input);
            string name = getNextName(i, input);
            while (!levelStack.empty() && levelStack.top() >= level) {
                length -= lengthStack.top();
                levelStack.pop();
                lengthStack.pop();
            }

            length += name.size();
            levelStack.push(level);
            lengthStack.push(name.size());

            if (isFile(name) && maxLength < length + level)
                maxLength = length + level;
        }

        return maxLength;
    }
};