题目描述

给定 n 个城市，编号为从 1 到 n。同时给你一个大小为 n-1 的数组 edges，其中 edges[i] = [u_i, v_i] 表示城市 u_i 和 v_i 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说，所有城市形成了一棵 树。

一棵 子树 是城市的一个子集，且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在，但在另一棵子树中不存在。

对于 d 从 1 到 n-1，请你找到城市间 最大距离 恰好为 d 的所有子树数目。

请你返回一个大小为 n-1 的数组，其中第 d 个元素（下标从 1 开始）是城市间 最大距离 恰好等于 d 的子树数目。

请注意，两个城市间距离定义为它们之间需要经过的边的数目。

样例

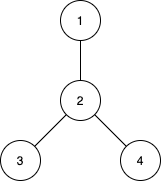
输入：n = 4, edges = [[1,2],[2,3],[2,4]]
输出：[3,4,0]
解释：
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。

输入：n = 2, edges = [[1,2]]
输出：[1]

输入：n = 3, edges = [[1,2],[2,3]]
输出：[2,1]

限制

• 2 <= n <= 15
• edges.length == n-1
• edges[i].length == 2
• 1 <= u_i, v_i <= n
• 题目保证 (u_i, v_i) 所表示的边互不相同。

算法

(暴力枚举，递归) $O(n2^n)$

1. 暴力枚举边集的子集，判断当前的子集是否构成一棵树。可以通过点的个数与边的个数的关系判断。
2. 如果当前子集构成了一棵树，则通过递归的方式来求解最长的距离。
3. 初始化一个数组 dis，记录每个点到其子树任意一个叶子节点的最长距离。任意选择一个点作为根节点开始递归求解。
4. 递归时，递归调用其子节点，然后通过子节点的最长距离来更新当前节点的最长距离。
5. 此时，如果当前节点有大于等于两个子节点，则找到子节点中最长和次长的 dis 再加 1，记为 m1 和 m2，那么则通过当前节点所能得到的最大距离就是 m1 + m2。
6. 如果当前节点只有一个子节点，则通过当前节点所能得到的最大距离就是 m1。如果当前节点为叶子节点，则不做考虑。

时间复杂度

• 共有 $O(2^{n-1})$ 种子集，递归判断遍历每个点一次，需要 $O(n)$ 的时间。
• 故总时间复杂度为 $O(n2^n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储临时的图和递归的系统栈。

C++ 代码

#define max(x, y) ((x) > (y) ? (x) : (y))

class Solution {
private:
    vector<int> dis;
    vector<vector<int>> graph;
    int maxDistance;

    void solve(int u, int fa) {
        int m1 = 0, m2 = 0;
        for (int v : graph[u]) {
            if (v == fa) continue;
            solve(v, u);

            dis[u] = max(dis[u], dis[v] + 1);

            if (m1 < dis[v] + 1) {
                m2 = m1;
                m1 = dis[v] + 1;
            } else if (m2 < dis[v] + 1) {
                m2 = dis[v] + 1;
            }
        }

        maxDistance = max(maxDistance, m1 + m2);
    }


public:
    vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {
        vector<int> ans(n - 1, 0);
        graph.resize(n);
        dis.resize(n);

        for (int mask = 1; mask < (1 << (n - 1)); mask++) {
            int numOfEdges = 0, numOfVertices = 0;
            for (int i = 0; i < n; i++)
                graph[i].clear();

            for (int i = 0; i < n - 1; i++)
                if (mask & (1 << i)) {
                    int u = edges[i][0] - 1, v = edges[i][1] - 1;
                    graph[u].push_back(v);
                    graph[v].push_back(u);
                    numOfEdges++;
                }

            int startVertex = -1;
            for (int i = 0; i < n; i++)
                if (graph[i].size() > 0) {
                    numOfVertices++;
                    startVertex = i;
                    dis[i] = 0;
                }

            if (numOfVertices != numOfEdges + 1)
                continue;

            maxDistance = 0;
            solve(startVertex, -1);

            ans[maxDistance - 1]++;
        }

        return ans;
    }
};