题目描述

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出从1号点到n号点的最多经过k条边的最短距离，如果无法从1号点走到n号点，输出impossible。

为什么Dijkstra算法对负权边会失效

Dijkstra算法使用了贪心的思想，本身就隐含了一个假设，如果当前结点1到2的距离不是最小的，从2出发的达到的点的距离也不是最小的

Dijkstra朴素算法代码：

int Dijkstra()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;

    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        st[t] = true;

        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }

    if (dist[n] == 0x3f3f3f3f)  return -1;
    return dist[n];
}

举例说明：

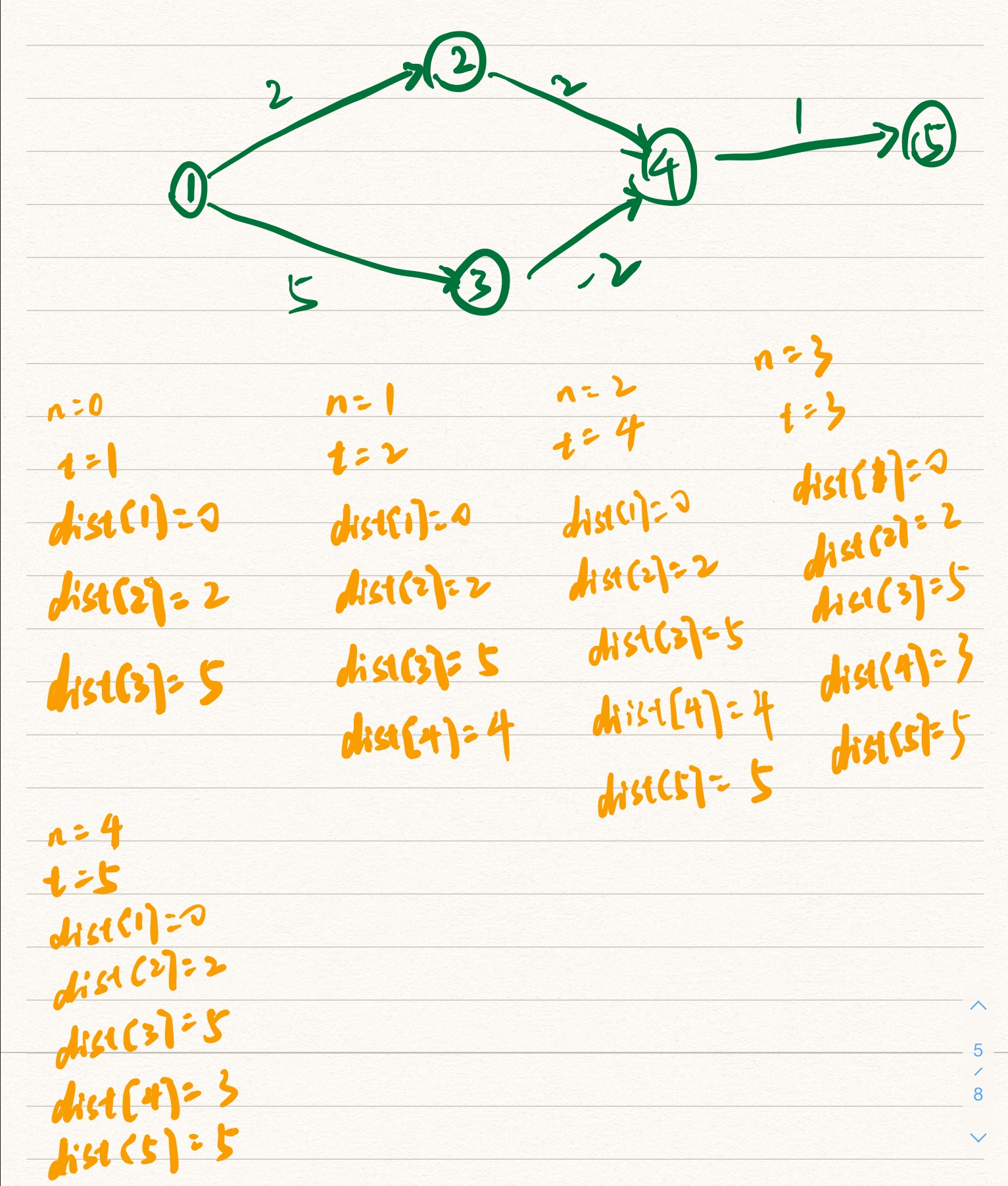
虽然t = 3时dist[4]更新为3，但是t = 4在t = 3前判断(贪心)，且g[3][5]为无穷，所以这里dist[5]并不会更新为4

为什么Bellman-Ford要使用backup数组记录dist数组上一个状态

因为题中有只经过k条边的限制，这里如果使用dist，串联会导致突破k条边的限制
使用备份数组，可以保证每次只更新一条边

Bellman-Ford算法的缺点

Bellman-Ford算法也可以解决边权都为正的情况，但是Bellman-Ford算法的时间复杂度为O(mn)，m条边，n个点，要是边数太多时间复杂度会过高

Bellman-Ford C++代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510, M = 100010;

int n, m, k;
int dist[N], backup[N];

struct Edge
{
    int a, b, w;
}edge[M];

int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < k; i ++ )   // 不超过k条边，所以迭代k次
    {
        // 备份数组，使每次只更新一条边，不会出现串联的结果，因为前面有只经过k条边的限制，这里如果使用dist，串联会导致突破k条边
        memcpy(backup, dist, sizeof backup);
        for (int j = 0; j < m; j ++ )
        {
            int a = edge[j].a, b = edge[j].b, w = edge[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2)  return -1;  // 有可能存在负权边,1到不了5和n号点，但是5到n可能是负权边可以更新
    return dist[n];
}

int main()
{
    cin >> n >> m >> k;

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        cin >> a >> b >> w;
        edge[i] = {a, b, w};
    }

    int t = bellman_ford();

    if (t == -1)    cout << "impossible" << endl;
    else    cout << t << endl;

    return 0;
}