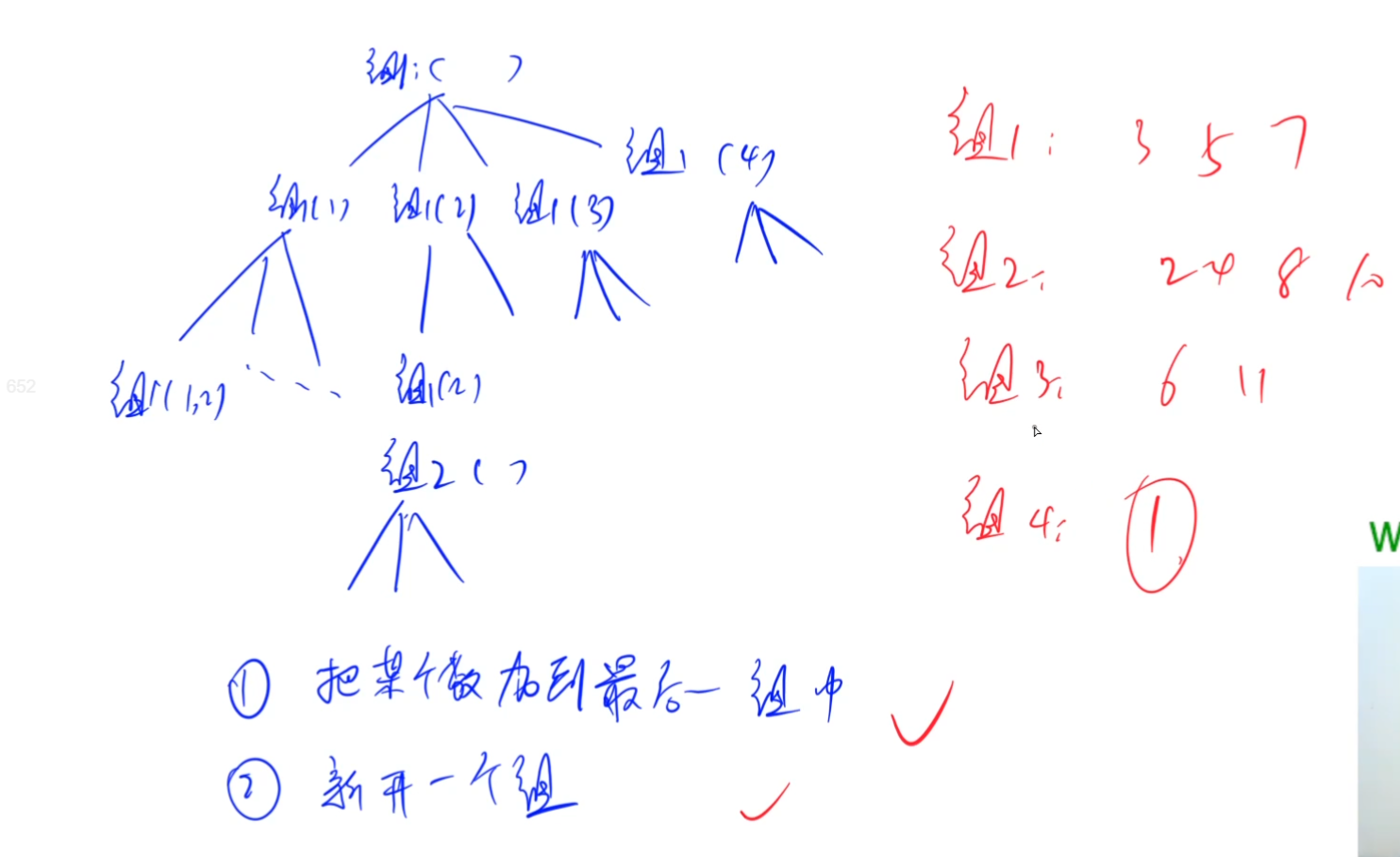
一组一组搜索，尽量把前一组填满，然后开新组。
比如说， 我们一共有枚举了三个组ga, gb, gc和一个新组gnew, 那么考虑元素p[i]。ga, gb已经把能加进来的元素都加进来了，p[i]还不在任何一个组(ga, gb) 内，就说明ga, gb考虑过，但基于最小组数的原则没有把p[i]加进来， 所以p[i]只能考虑加入到gc或者gnew

如果最后一组，新开的一组都能放，则放置在最后一组，因为答案求的是最小组数，所以尽可能少开新组。

组3：

放1，2， 3

放2， 1， 3

放3， 2， 1

都是一样的，所以求的是组合数

所以如何递归实现组合型枚举

我们按照从小到大顺序开始枚举

#include <cstring>
#include <iostream>

using namespace std;

const int N = 10;

int n;
int p[N];
int group[N][N];
bool st[N];
int ans = N;

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

bool check(int group[], int gc, int i) {
    // 如果组内的p[group[j]]与正在枚举的p[i]  存在 >1 的公因子， 则不互质
    for (int j = 0; j < gc; j++)
        if (gcd( p[group[j]] , p[i] ) > 1)
            return false;
    return true;
}

// 组的序号g， 当前组内下标gc，当前一共tc个元素， 下标从start开始搜索
void dfs(int g, int gc, int tc, int start) {
    if (g >= ans) return;
    if (tc == n) ans = g;

    bool flag = true;
    // 从start开开始搜索， 并且没有被搜索过的下标i
    for (int i = start; i < n; i++)
        if (!st[i] && check(group[g], gc, i)) {
            st[i] = true;
            group[g][gc] = i;
            dfs(g, gc + 1, tc + 1, i + 1);
            st[i] = false;

            flag = false;
        }

    if (flag) dfs(g + 1, 0, tc, 0);
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> p[i];

    //第1组，组内有0个元素， 当前搜了0个元素， 从0号下标开始搜
    dfs(1, 0, 0, 0);

    cout << ans << endl;

    return 0;
}