题目描述

在 W 星球上有 n 个国家。

为了各自国家的经济发展，他们决定在各个国家之间建设双向道路使得国家之间连通。

但是每个国家的国王都很吝啬，他们只愿意修建恰好 n – 1 条双向道路。

每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端的国家个数之差的绝对值。

例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2 – 4|=2，图中圆圈里的数字表示国家的编号。

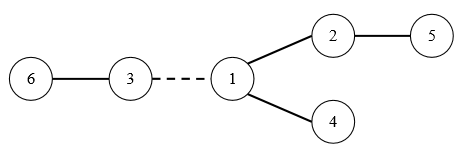
由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计算出所需要的费用。

请你帮助国王们设计一个这样的软件。

输入格式
输入的第一行包含一个整数 n，表示 W 星球上的国家的数量，国家从 1 到 n 编号。

接下来 n – 1 行描述道路建设情况，其中第 i 行包含三个整数 ai、bi 和 ci，表示第 i 条双向道路修建在 ai 与 bi 两个国家之间，长度为 ci。

输出格式
输出一个整数，表示修建所有道路所需要的总费用。

数据范围
所有测试数据的范围和特点如下表所示

QQ截图20190905151620.png

输入样例：
6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1
输出样例：
20
注意
为了防止DFS解法爆栈，本题只加入了前14个测试点，进行测试。

算法1

(暴力DFS)

思路很简单，首先创建邻接表，循环读入数据，然后遍历整个邻接表头节点，依次双向DFS每个头节点连接的点并返回两个计数器，利用公式计算即可。此处遇到的第一个坑是：本题没有说明图上所有的点均处于联通状态，因此不可使用变形公示计算(即长度*|总节点数-（2 * 单侧节点数）|)，因为多个点可以独立构成图，整图可由多个子图构成，所以不得不遍历两次得到两侧节点数。此处已经参与过计算的边长度标记为0，作为已访问的标志。第二个坑接踵而至，因为循环的多层嵌套、搜索数据太多导致时间复杂度直线向上跑，结果后几个测试点全超时了。。。可以算得上是爆搜失败的经典案例了，此处贴上代码作为参考
如有邻接表的优解方案，请各位大佬指教

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>
#define NODELEN sizeof(node) 
typedef long long ll;
using namespace std;

typedef struct node{
    ll serial;
    ll len;
    struct node * next;
}node;

bool *vis;  //访问记录数组，记得用完重置状态


//初始化邻接表，节点0废置不用，返回头指针
node *init(ll n){
    node *storage = (node *)malloc((n + 1) * NODELEN);
    vis = (bool *)malloc((n + 1) * sizeof(bool));
    for(ll i = 0; i <= n; i++){
        storage[i].serial = i;
        storage[i].len = 0;
        storage[i].next = NULL;
        vis[i] = false;
    }
    return storage;
}

//创建邻接表
bool create_path(node *data, ll n, ll source, ll target, ll len){
    node *tmp = (node *)malloc(NODELEN);
    tmp -> serial = target;
    tmp -> len = len;
    tmp -> next = NULL;

    node *now = & data[source];
    while(now -> next != NULL) now = now -> next;  //指针移动到表尾处，尾插节点
    now -> next = tmp;
    return true;
}

//删除节点(注意双向删除)
void del_node(node *data, ll source, ll target){
    node *now = & data[source];
    while(now -> next != NULL && now -> serial != target) now = now -> next;
    now -> len = 0;  
}

//计算每条道路花费的费用并返回
ll ans(ll cnt1, ll cnt2, ll len){
    if(len == 0) return 0;
    return len * llabs(cnt1 - cnt2);
}

//深度优先搜索&计数变量
ll nod_cnt = 0;
//深度优先搜索解决问题：定向搜索节点数目
void dfs(node *data, ll source, ll target){
    node *tmp = & data[target];
    vis[source] = true;
    vis[target] = true;
    nod_cnt ++;
    while(tmp -> next != NULL){
        tmp = tmp -> next;
        if(!vis[tmp->serial]) dfs(data, target, tmp->serial);
        else continue;
    }
    return;
}

//求解题目-最终解
ll solve(node *data, int n){
    ll fee = 0;
    for(ll i = 1; i <= n; i++){
        node *now = & data[i];
        while(now -> next != NULL){
            now = now -> next;

            if(now -> len == 0) continue;
            //状态重置
            nod_cnt = 0;
            for(int j = 0; j <= n; j++) vis[j] = false;
            //正向搜索
            dfs(data, i, now -> serial);
            ll cnt1 = nod_cnt;

            //状态重置
            nod_cnt = 0;
            for(int j = 0; j <= n; j++) vis[j] = false;
            //反向搜索
            dfs(data, now -> serial, i);
            ll cnt2 = nod_cnt;

            fee += ans(cnt1, cnt2, now -> len);
            del_node(data, i, now -> serial);
            del_node(data, now -> serial, i);         
        }
    }
    return fee;
}

int main(){
    ll n = 0;
    cin >> n;
    node *data = init(n);
    for(ll i = 0, s, t, len; i < n - 1; i++){
        cin >> s >> t >> len;
        if(create_path(data, n, s, t, len) && create_path(data, n, t, s, len)) continue;
        else break;
    }
    cout << solve(data, n) << endl;
    system("pause");
    return 0;
}

算法2

(树上DFS)

在参考了 的解法后简单复现了一下，发现选对储存结构真的很关键，这里贴上能够AC的代码，同样参考自原作者
思路依旧很简单：把无根树转成有根树，记录每个点的size(以它为根的子树含有多少结点)，然后再从根dfs一遍整棵树即可

C++ 代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef long long LL;
int v[2000005]={0},w[2000005]={0},first[1000005]={0},next[2000005]={0},size[1000005]={0};
LL cost[2000005]={0};
int n,e=0;
void tj(int x,int y,int z)
{
    v[++e]=y;
    w[e]=z;
    next[e]=first[x];
    first[x]=e;
}
void dfs(int x,int fa)
{
    int i;
    size[x]=1;
    for(i=first[x];i!=0;i=next[i])
        if(v[i]!=fa)
        {
            dfs(v[i],x);
            size[x]+=size[v[i]];
        }
}
void getcost(int x,int fa)
{
    int i;
    for(i=first[x];i!=0;i=next[i])
        if(v[i]!=fa)
        {
            cost[i]=(LL)w[i]*(LL)abs(n-size[v[i]]*2);
            getcost(v[i],x);
        }
}
int main()
{
    LL ans=0;
    int i,x,y,z;
    scanf("%d",&n);
    for(i=1;i<n;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        tj(x,y,z);
        tj(y,x,z);
    }
    dfs(1,0);
    getcost(1,0);
    for(i=1;i<=e;i++)
        ans+=cost[i];
    printf("%lld",ans);
    return 0;
}