题目描述

给定一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点 可以 重合。

请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 10^9 + 7 取余 后返回。

样例

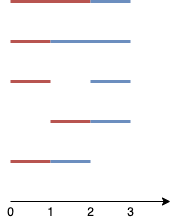
输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案
{(0,2),(2,3)}
{(0,1),(1,3)}
{(0,1),(2,3)}
{(1,2),(2,3)}
{(0,1),(1,2)}。

输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 10^9 + 7 取余得到 796297179 。

输入：n = 5, k = 3
输出：7

输入：n = 3, k = 2
输出：1

限制

• 2 <= n <= 1000
• 1 <= k <= n-1

算法

(动态规划) $O(nk)$

1. 设状态 $f(i, j)$ 表示当前到了坐标 $i$ 且使用了 $j$ 个不重复线段的方案数。$i$ 的下标从 0 开始。
2. 初始时，$f(0, 0) = 1$，其余为 0。
3. 转移时，对于 $f(i, j)$
   • 坐标 $i$ 可以不设置线段终点：$f(i, j) = f(i, j) + f(i - 1, j)$。
   • 如果 $j > 0$，则坐标 $i$ 设置为线段终点，此时可以枚举坐标起点 $s$：$f(i, j) = f(i, j) + \sum_{s=0}^{i-1}{f(s, j - 1)}$。
4. 最终答案为 $f(n - 1, k)$。
5. 由于需要枚举 $s$ 会导致时间复杂度上升，故添加一个辅助数组 $g(i, j) = \sum_{s=0}^{i}{f(i, j)}$。
6. 此时第二种转移可以写成，$f(i, j) = f(i, j) + g(i - 1, j - 1)$。枚举转移完成后维护 $g(i, j) = g(i - 1, j) + f(i, j)$。

时间复杂度

• 状态数为 $O(nk)$，带有辅助数组的转移时间为常数，故总时间复杂度为 $O(nk)$。

空间复杂度

• 需要 $O(nk)$ 的空间存储状态。

C++ 代码

class Solution {
public:
    int numberOfSets(int n, int k) {
        const int mod = 1000000007;
        vector<vector<int>> f(n, vector<int>(k + 1, 0));
        vector<vector<int>> g(n, vector<int>(k + 1, 0));

        f[0][0] = 1;
        g[0][0] = 1;
        for (int i = 1; i < n; i++)
            for (int j = 0; j <= k; j++) {
                f[i][j] = f[i - 1][j];
                if (j > 0)
                    f[i][j] = (f[i][j] + g[i - 1][j - 1]) % mod;

                g[i][j] = (g[i - 1][j] + f[i][j]) % mod;
            }

        return f[n - 1][k];
    }
};