题目描述

给定一个数组 towers 和一个整数 radius，数组中包含一些网络信号塔，其中 towers[i] = [x_i, y_i, q_i] 表示第 i 个网络信号塔的坐标是 (x_i, y_i) 且信号强度参数为 q_i。所有坐标都是在 X-Y 坐标系内的 整数 坐标。两个坐标之间的距离用 欧几里得距离 计算。

整数 radius 表示一个塔 能到达 的 最远距离。如果一个坐标跟塔的距离在 radius 以内，那么该塔的信号可以到达该坐标。在这个范围以外信号会很微弱，所以 radius 以外的距离该塔是 不能到达的。

如果第 i 个塔能到达 (x, y)，那么该塔在此处的信号为 ⌊q_i / (1 + d)⌋，其中 d 是塔跟此坐标的距离。一个坐标的 网络信号 是所有 能到达 该坐标的塔的信号强度之和。

请你返回 网络信号 最大的整数坐标点。如果有多个坐标网络信号一样大，请你返回字典序最小的一个坐标。

注意

• 坐标 (x1, y1) 字典序比另一个坐标 (x2, y2) 小：要么 x1 < x2，要么 x1 == x2 且 y1 < y2。
• ⌊val⌋ 表示小于等于 val 的最大整数（向下取整函数）。

样例

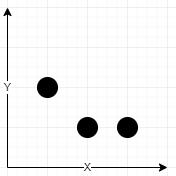
输入：towers = [[1,2,5],[2,1,7],[3,1,9]], radius = 2
输出：[2,1]
解释：
坐标 (2, 1) 信号强度之和为 13
- 塔 (2, 1) 强度参数为 7 ，在该点强度为 ⌊7 / (1 + sqrt(0)⌋ = ⌊7⌋ = 7
- 塔 (1, 2) 强度参数为 5 ，在该点强度为 ⌊5 / (1 + sqrt(2)⌋ = ⌊2.07⌋ = 2
- 塔 (3, 1) 强度参数为 9 ，在该点强度为 ⌊9 / (1 + sqrt(1)⌋ = ⌊4.5⌋ = 4
没有别的坐标有更大的信号强度。

输入：towers = [[23,11,21]], radius = 9
输出：[23,11]

输入：towers = [[1,2,13],[2,1,7],[0,1,9]], radius = 2
输出：[1,2]

输入：towers = [[2,1,9],[0,1,9]], radius = 2
输出：[0,1]
解释：坐标 (0, 1) 和坐标 (2, 1) 都是强度最大的位置，但是 (0, 1) 字典序更小。

限制

• 1 <= towers.length <= 50
• towers[i].length == 3
• 0 <= x_i, y_i, q_i <= 50
• 1 <= radius <= 50

算法

(暴力枚举) $O(n \ times 50^2)$

1. 根据数据范围，最小可能的坐标为 (0, 0)，最大可能的坐标为 (50, 50)。这是因为最优点不可能超出所有塔构成的凸包。
2. 暴力枚举 [0, 50] x [0, 50] 内的每个整数坐标，然后按照题意描述模拟。

时间复杂度

• 待枚举点的个数为 $50^2$，每次枚举需要 $O(n)$ 的时间计算，故总时间复杂度为 $O(n \ times 50^2)$。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

class Solution {
private:
    int squareDis(int x1, int y1, int x2, int y2) {
        return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
    }

public:
    vector<int> bestCoordinate(vector<vector<int>>& towers, int radius) {
        vector<int> ans(2);
        int maxDis = 0;

        for (int i = 0; i <= 50; i++)
            for (int j = 0; j <= 50; j++) {
                int totDis = 0;
                for (const auto &t : towers) {
                    int sd = squareDis(i, j, t[0], t[1]);
                    if (sd <= radius * radius)
                        totDis += int(floor(t[2] / (1 + sqrt(sd))));
                }
                if (maxDis < totDis) {
                    maxDis = totDis;
                    ans[0] = i; ans[1] = j;
                }
            }

        return ans;
    }
};