题目大意

求一个字符串的最长回文子串长度，多测。

解题思路

是 Manacher 算法的模板题。

Manacher

解决问题

最长回文子串：给定一个字符串，求它的最长回文子串长度。

原理

从中心扩展延伸的方法的缺陷：处理字符串长度的奇偶性带来的对称轴不确定问题

解决方案，对原来的字符串进行处理，在首尾和所有空隙插入一个无关字符，插入后不改变原串中回文的性质，但串长都变成了奇数.

定义：回文半径：一个回文串中最左或最右位置的字符到其对称轴的距离 ，用 $p[i]$ 表示第 $i$ 个字符的回文半径.

    char : # a # b # c # b # a #
    p[i] :   1 2 1 2 1 6 1 2 1 2 1
p[i] - 1 : 0 1 0 1 0 5 0 1 0 1 0
       i :      1 2 3 4 5 6 7 8 9 10 11

显然，最大的 $p[i]−1$ 就是答案

插入完字符之后对于一个回文串的长度为 原串长度*2+1，等于 这个回文串回文半径*2+1，显然相等。

这样问题就转换成了怎样快速的求出 $p$.用 $mx$ 表示所有字符产生的最大回文子串的最大右边界， $id$ 表示产生这个边界的对称轴位置。

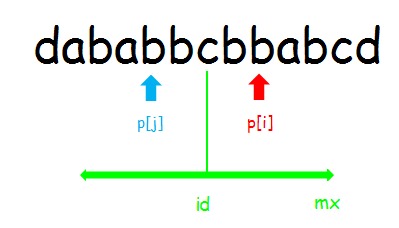
设已经求出了$p[1…7]$ ，当 $i<mx$ ，因为 $id$ 被更新过了，而 $i$ 是 $id$ 之后的位置，第 $i$ 个字符一定落在 $id$ 右边。

记 串 $i$ 表示以 $i$ 为对称轴的回文串，$j$ 和 $id$ 同理。

情况1：i < mx

利用回文串的性质，对于 $i$ ，可以找到一个关于 $id$ 对称的位置 $j=id∗2−i$ ，进行加速查找
(1)

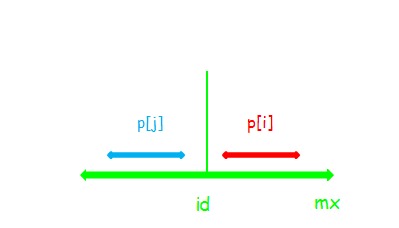
显然 $p[i]=p[j]$ ，串 $i$ 不可以再向两边扩张。如果可以的话，$p[j]$ 也可以再扩张，而 $p[j]$ 已经确定了。
(2)

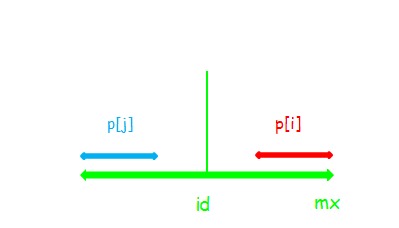
此时 $p[i]=p[j]$ ,与(1)不同的是，串 $i$ 是可以再扩张的。
(3)

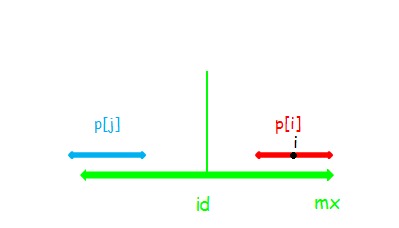
此时 $p[i]=mx−i$ ,这时只能确定 串 $i$ 在 $mx$ 以内的部分是回文的，并不能确定串 $i$ 和 串 $j$ 相同。
同样，这时串 $i$ 是不可以再向两端扩张的。

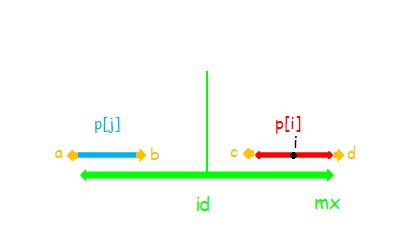
如果可以扩张，如图（这里的假设是 $p[j]>p[i]$ ，那么 $p[j]\ge p[i]+1$ ，截取 $a,b$ 使得和扩张 $1$ 之后的 $i$ 相同显然不会影响正确性），则 $d=c$ ，根据对称性 $c=b$ ，又因为 $a=b$ ，所以 $a=d$ ，串 $id$ 可以继续扩张，但 $p[id]$ 已经固定了.

情况2：i >= mx

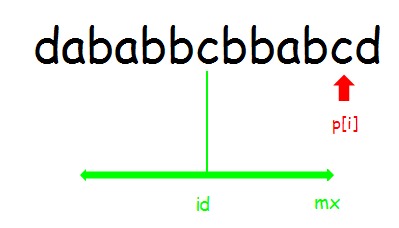
$p[i]=1$

注意，这里的 $p[i]$ 的情况讨论均指“可以从 $id$ 和 $mx$ 中继承”的部分，也就是已经处理过的部分不会再进行处理，要处理一定是往后拓展，而不是最终的结果，如果不理解可以看看代码。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=22000010;
char s[N],str[N];
int pos[N];

int init()              //处理原字符串
{
        int len=strlen(s); 
        str[0]='@'; str[1]='#';         //@是防止越界
        int j=2;
        for ( int i=0; i<len; i++ )
                str[j++]=s[i],str[j++]='#';
        str[j]='\0'; return j;
}

int manacher()
{
        int ans=-1,len=init(),mx=0,id=0;
        for ( int i=1; i<len; i++ )
        {
                if ( i<mx ) pos[i]=min( pos[id*2-i],mx-i );             //situation1
                else pos[i]=1;                                  //situation2
                while ( str[i+pos[i]]==str[i-pos[i]] ) pos[i]++;                //扩展  
                if ( pos[i]+i>mx ) mx=pos[i]+i,id=i;            //update id
                ans=max( ans,pos[i]-1 );
        }
        return ans;
}

int main()
{
        int cnt=0;
        while ( scanf( "%s",s) && s[0]!='E' ) 
                printf( "Case %d: %d\n",++cnt,manacher() );
}