题目描述

假设城堡地面是 n×n个方格。如下图所示。

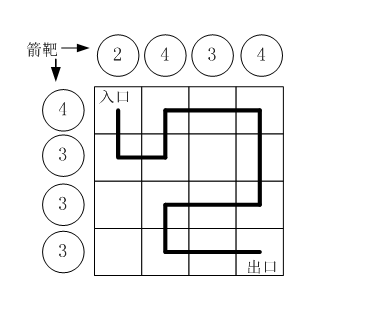
1.骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。

2.每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有n个靶子）同一个方格只允许经过一次。但不必走完所有的方格。

3.本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）。

dfs+回溯+剪枝

先来看看题意：

1.从西北角到东南角->（0,0）到（n-1,n-1）

2.只能上下左右四个方向移动，对角线和闪现是不允许的（这骑士太弱了吧，快速移动都不会）

3.每走到一个新的格子（r,c），向对应的行（第r行）和列（第r列）各射一箭

4.骑士不会吃回头草->走过的格子不会再走

题意明了后，有经验的小伙伴肯定会有搜索这个思路，如果你还没有，请不要着急，这只是时间问题，只要做题做多了，你也会有的。

关键点

1.二维数组（r,c）-> 一维数组转换：r*列数+c

2.每走一步射两箭->总步数=（箭的总数）/2

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N = 25;
int R[N],C[N];
int n,resSize;//resSize就是总步数
bool st[N*N];//n行n列有n*n个点
vector<int> path;
int gr[4]={-1,0,1,0},gc[4]={0,1,0,-1};

void dfs(int r,int c){
    //到达终点且总步数达标,输出并返回
    if(r*n+c==n*n-1&&path.size()==resSize){
        for(int i=0;i<path.size();i++){
            printf("%d",path[i]);
            if(i!=path.size()-1){
                printf(" ");
            }
        }
        return ;
    }
    for(int i=0;i<4;i++){
        int nr=r+gr[i],nc=c+gc[i];
        //nr>=0,nr<n,nc>=0,nc<n 基本边界判断
        //R[nr]>0,C[nc]>0,要走的点必须得有箭，没箭不走
        //nr*n+nc 二维转一维
        //!st[nr*n+nc] 这个点走没走过的判断
        if(nr>=0&&nr<n&&nc>=0&&nc<n&&R[nr]&&C[nc]&&!st[nr*n+nc]){
            //都满足，状态更新
            R[nr]--,C[nc]--;
            st[nr*n+nc]=true;
            path.push_back(nr*n+nc);
            //进行尝试
            dfs(nr,nc);
            //状态恢复
            path.pop_back();
            st[nr*n+nc]=false;
            R[nr]++,C[nc]++;
        }
    }
}
int main(){
    scanf("%d",&n);
    int sum=0;
    for(int i=0;i<n;i++){
        scanf("%d",&C[i]);
        sum+=C[i];
    }
    for(int i=0;i<n;i++){
        scanf("%d",&R[i]);
        sum+=R[i];
    }
    resSize=sum/2;
    //起点必须经过，所以可以先对r,c,st,path进行一些处理
    R[0]--,C[0]--;
    st[0]=true;
    path.push_back(0);

    dfs(0,0);
    return 0;
}

我的朋友，如果你对代码表示难以理解，这边建议先对y总算法基础课的第三讲的DFS和BFS小节进行学习和复习喵！