题目描述

代码来自yxc大佬的视频，自己写了一份速度缓慢的代码再来阅读该代码，只能惊呼精简高效！！！

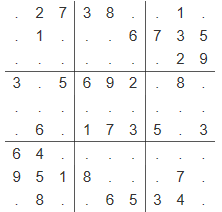
数独是一种传统益智游戏，你需要把一个9 × 9的数独补充完整，使得图中每行、每列、每个3 × 3的九宫格内数字1~9均恰好出现一次。

请编写一个程序填写数独。

输入格式
输入包含多组测试用例。

每个测试用例占一行，包含81个字符，代表数独的81个格内数据（顺序总体由上到下，同行由左到右）。

每个字符都是一个数字（1-9）或一个”.”（表示尚未填充）。

您可以假设输入中的每个谜题都只有一个解决方案。

文件结尾处为包含单词“end”的单行，表示输入结束。

输出格式
每个测试用例，输出一行数据，代表填充完全后的数独。

样例

输入样例：
.2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end
输出样例：
527389416819426735436751829375692184194538267268174593643217958951843672782965341
416837529982465371735129468571298643293746185864351297647913852359682714128574936

算法1

时间卡的比较紧,搜索上做了许多优化

1 进行可填写数据的筛选.由于数独本身的性质，1~9同一数字不能在同一行 同一列 同一九宫格出现两次以上。
我开始计划是开一个 9*9的数组记录每个格子可能出现的数字.每次确认填写一个数字 就更新同行同列同九宫格里的记录
但是这样的话，每次填写一个数字及需要更新 一行9个 一列9个 和九宫格九格的数据。共27个数据。
YXC大佬的代码 使用的 行记录一个 列记录一个 九宫格记录一个 这样只需要更新三个数据即可

2 优化填写格子的策略，每个格子可填写的数据比较少的优先选取。 这也是剪枝的一种.
代码见

    //找到可选方案数最少的空格
    int minv = 10;
    int x, y;
    for(int i = 0;i < N;i++)
        for(int j = 0;j < N;j++)
            if (str[i*9+j] == '.') {
                int t = ones[get(i, j)];
                if (t < minv) {
                    minv = t;
                    x = i, y = j;
                }
            }

3 一些其他小技巧，使用位来记录该空格可填写那些数字
000000001 表示可填写1
000000010 表示可填写2
000000100 表示可填写3
000000101 表示可填写1和3
......
x = 000000111 表示可填写1 2 3。 如果我们当前选择填写2 那么只要 x - (1<<(2-1))就可以把填写2的表示去除了
代码里不是2-1 而是 可填写的数字的字母的实际值与 ‘1’的差值

4 判断是否是统一九宫格 采用 x/3==i/3 y/3 == j/3

还有其他一些小技巧 欢迎一起讨论

C++ 代码

#include <iostream>
#include <map>
#include <vector>
#include <string>
#include <stdio.h>

using namespace std;



/*
.2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end
*/


const int N = 9;

int map1[1 << N];
int Xarr[N];
int Yarr[N];
int SameXYArr[N / 3][N / 3];

int ones[1 << N], map[1 << N];

char str[100];

void Init()
{
    for (int i = 0; i < N; i++) {
        Xarr[i] = (1 << N) - 1;
        Yarr[i] = (1 << N) - 1;
        map1[1 << i] = i;
    }

    for (int i = 0; i < N / 3; i++) {
        for (int j = 0; j < N / 3; j++) {
            SameXYArr[i][j] = (1 << N) - 1;
        }
    }
}

inline int lowbit(int x) {
    return x & -x;
}

inline int get(int x, int y)
{
         return Xarr[x] & Yarr[y] & SameXYArr[x / 3][y / 3];
}

bool Dfs(int count, char str[])
{
    if (!count) return true;

    int minv = 10;
    int minx = -1; int miny = -1;

    for (int x = 0; x < 9; x++) {
        for (int y = 0; y < 9; y++)
        {
            if (str[x * 9 + y] == '.') {
                int t = ones[get(x,y)];

                if (t < minv) {
                    minv = t;
                    minx = x;
                    miny = y;
                }
            }
        }
    }

    if (0 == minv)
        return false;

    int tryNums = get(minx, miny);


    while (tryNums != 0) {
        int trynum = map1[lowbit(tryNums)];

        Xarr[minx] -= 1 << trynum;
        Yarr[miny] -= 1 << trynum;
        SameXYArr[minx / 3][miny / 3] -= 1 << trynum;
        str[minx * 9 + miny] = '1' + trynum;

        if (Dfs(count - 1, str))  return true;

        //回复现场
        Xarr[minx] += 1 << trynum;
        Yarr[miny] += 1 << trynum;
        SameXYArr[minx / 3][miny / 3] += 1 << trynum;
        str[minx * 9 + miny] = '.';

        tryNums -= lowbit(tryNums);
    }

    return false;
}

void Do(char str[])
{
    Init();
    int count = 0;
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            if (str[i * 9 + j] != '.') {
                int idx = 1 << (str[i * 9 + j] - '1');
                Xarr[i] -= idx;
                Yarr[j] -= idx;
                SameXYArr[i / 3][j / 3] -= idx;
            }
            else {
                count++;
            }
        }
    }

    Dfs(count, str);
    cout << str << endl;

    return;
}


int main()
{
    ios::sync_with_stdio(false);

    for (int i = 0; i < N; i++) map1[1 << i] = i;
         for (int i = 0; i < 1 << N; i++) {
                 int s = 0;
                 for (int j = i; j; j -= lowbit(j)) s++;
                 ones[i] = s; //i的二进制表示中有s个1

    }

        while (cin >> str, str[0] != 'e') {
            //s = ".2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.";

            Do(str);
        }


}