LeetCode04 寻找两个正序数组的中位数

题目描述

给定两个大小为 m 和 n的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

样例

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

算法分析

中位数：奇数就是中间那个、偶数是中间两个的平均值

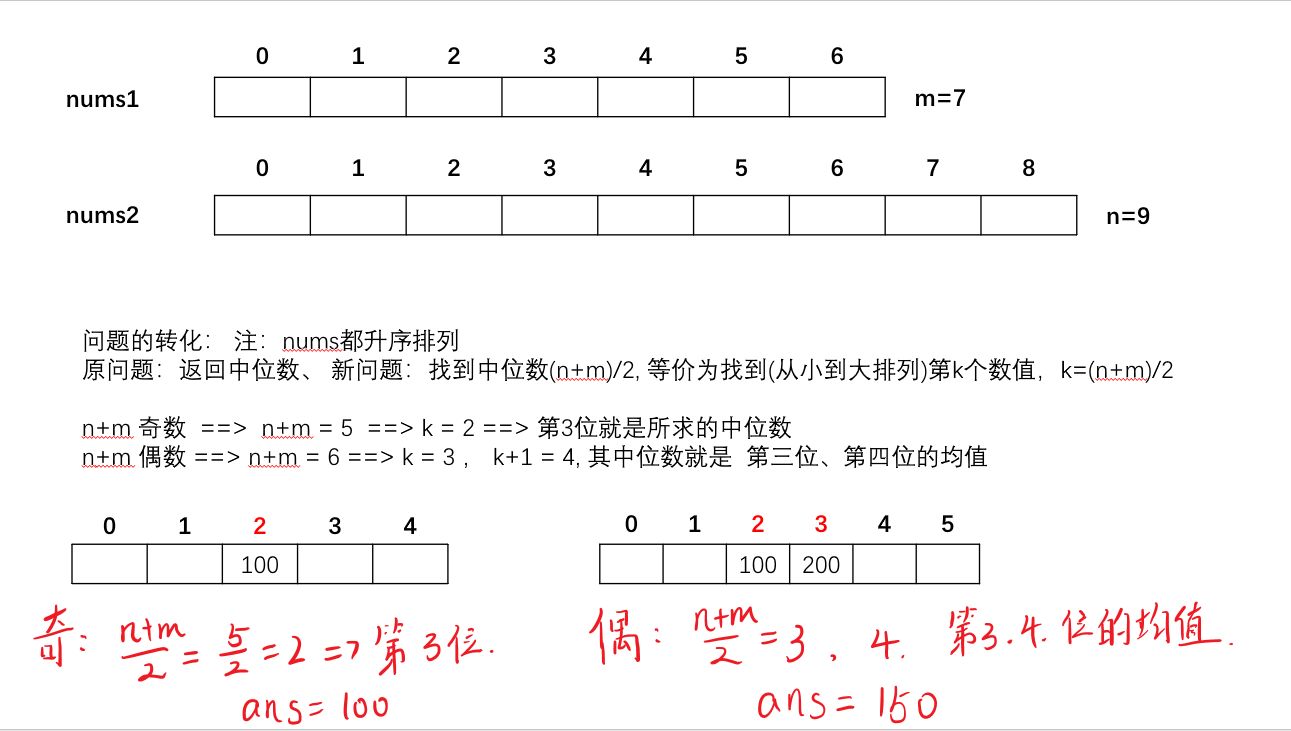
• 问题转化为找第k个数
• 一共奇数个时候。找到第total/2 +1 个
• 一共奇数个时候，找到第total/2和total/2 + 1这这两个数，取均值

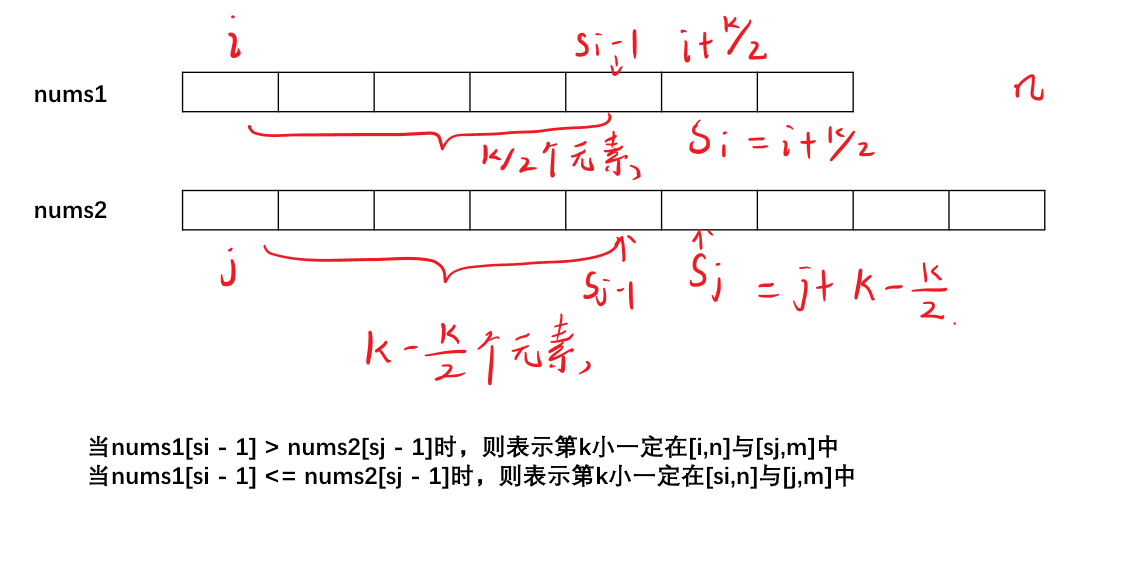
如何找第k个数值？

• 默认第一个数组的长度小于第二个数组的长度，如果否，就反转一下
• 当nums1[si - 1] > nums2[sj - 1]时，则表示第k小一定在[i,n]与[sj,m]中
• 当nums1[si - 1] <= nums2[sj - 1]时，则表示第k小一定在[si,n]与[j,m]中

时间复杂度

$O(n+m)$

Java代码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int total = nums1.length + nums2.length;
        if(total % 2 == 0){
            int left  = f(nums1, 0, nums2, 0, total/2);
            int right = f(nums1, 0, nums2, 0, total/2 + 1);
            return (left + right) / 2.0;
        }else{
            return f(nums1, 0, nums2, 0, total/2 + 1);
        }
    }


    static int f(int[] nums1, int i, int[] nums2, int j, int k){
        //默认是第一个数组是更短的
        if(nums1.length - i > nums2.length - j){
            return f(nums2, j, nums1, i, k);
        } 

        //第一个数组已经用完了
        //现在的第k个就是 nums[j+k-1],  nums[j]是第一个
        if(nums1.length == i) return nums2[j+k-1];

        //当k==1 k==1 说明就是这一个
        if(k==1) return Math.min(nums1[i], nums2[j]);

        int si = Math.min(nums1.length, i + k/2);
        int sj = j + k - k/2; //这里不用Max.min,sj一定不会超过nums[2].length

        if(nums1[si - 1] > nums2[sj - 1]){
            //[i~n] 和 [sj~m]  k-(sj-j)个
            return f(nums1,i,nums2,sj,k - (sj - j));
        }else{
            //[si~n] 和 [j~m] k-(si-i)个
            return f(nums1,si,nums2,j,k - (si - i));
        }
    }
}