一个建图的小优化

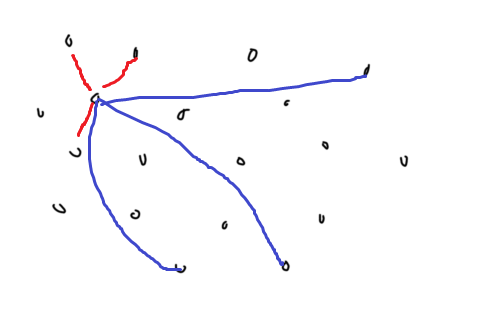
如上图所示：
在建立最少生成树时，最终的边实际上是每个点周围邻域中的边(红色所示)，而蓝色边是没用的“废边”。
在未优化前，实际上建立了一张完全图，这样的边数是n^2量级。最小生成树是一张稀疏图，有效可选边应是边数为n量级的稀疏图。
因此，有了一个下面非常初级的优化，计算图中最大边，然后在建边时只选择长度远小于最大边值的边。
未做优化前运行时间128ms，优化后22ms。
这里，希望yxc和其他大佬能够留言解答，如何“局域性质的”建立有效边，有没有相关算法。
代码：

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 510, M = N * N / 2;

typedef pair<int, int> PII;

struct Edge {
    int x, y;
    double w;

    bool operator<(const Edge &e) const {
        return w < e.w;
    }
} edges[M];

int n, k, p[N], m;

PII q[M];

int find(int x) {
    return p[x] == x ? x : p[x] = find(p[x]);
}

double getDist(PII &a, PII &b) {
    int dx = a.first - b.first, dy = a.second - b.second;
    return sqrt(dx * dx + dy * dy);
}


int main() {
    cin >> n >> k;
    int lr = 1e9, lc = 1e9, hr = 0, hc = 0;
    for (int i = 1; i <= n; i++) p[i] = i;
    for (int i = 0; i < n; i++) {
        cin >> q[i].first >> q[i].second;
        lr = min(lr, q[i].first);
        lc = min(lc, q[i].second);
        hr = max(hr, q[i].first);
        hc = max(hc, q[i].second);
    }
    PII x = {lr, lc}, y = {hr, hc};
    double tot = getDist(x, y) / 10;
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++) {
            double t = getDist(q[i], q[j]);
            if (t > tot && n > 50) continue;
            edges[m++] = {i, j, t};
        }
    sort(edges, edges + m);
    int cnt = n;
    double res = 0;
    for (int i = 0; i < m; i++) {
        if (cnt <= k) break;
        int a = find(edges[i].x), b = find(edges[i].y);
        if (a != b) {
            cnt--;
            p[a] = b;
            res = edges[i].w;
        }
    }
    printf("%.2lf\n", res);
    return 0;
}