题目描述

Chef Monocarp has just put n dishes into an oven. He knows that the i-th dish has its optimal cooking time equal to ti minutes.

At any positive integer minute T Monocarp can put no more than one dish out of the oven. If the i-th dish is put out at some minute T, then its unpleasant value is |T−ti| — the absolute difference between T and ti. Once the dish is out of the oven, it can’t go back in.

Monocarp should put all the dishes out of the oven. What is the minimum total unpleasant value Monocarp can obtain?

Input
The first line contains a single integer q (1≤q≤200) — the number of testcases.

Then q testcases follow.

The first line of the testcase contains a single integer n (1≤n≤200) — the number of dishes in the oven.

The second line of the testcase contains n integers t1,t2,…,tn (1≤ti≤n) — the optimal cooking time for each dish.

The sum of n over all q testcases doesn’t exceed 200.

Output
Print a single integer for each testcase — the minimum total unpleasant value Monocarp can obtain when he puts out all the dishes out of the oven. Remember that Monocarp can only put the dishes out at positive integer minutes and no more than one dish at any minute.

Note
In the first example Monocarp can put out the dishes at minutes 3,1,5,4,6,2. That way the total unpleasant value will be |4−3|+|2−1|+|4−5|+|4−4|+|6−5|+|2−2|=4.

In the second example Monocarp can put out the dishes at minutes 4,5,6,7,8,9,10.

In the third example Monocarp can put out the dish at minute 1.

In the fourth example Monocarp can put out the dishes at minutes 5,1,2,4,3.

In the fifth example Monocarp can put out the dishes at minutes 1,3,4,5.

样例

6
6
4 2 4 4 5 2
7
7 7 7 7 7 7 7
1
1
5
5 1 2 4 3
4
1 4 4 4
21
21 8 1 4 1 5 21 1 8 21 11 21 11 3 12 8 19 15 9 11 13

4
12
0
0
2
21

这是一个dp问题 咱们可以用y氏dp分析法来分析这个问题
设dp[i][j]表示 我前i道菜在j时间拿完产生的不高兴的最小值
经过y氏大法分析 dp[i,j]=min(dp[i-1,i-1~j-1]);
然后注意一下数据范围
题目中所给的n是小于等于200 对于最后一个菜我最晚可以在400时刻拿出来
然后注意一下初始化 因为第一道菜 是退化成 i-1来算的 所以可以拿出来的最小值是0时刻
分析图解：

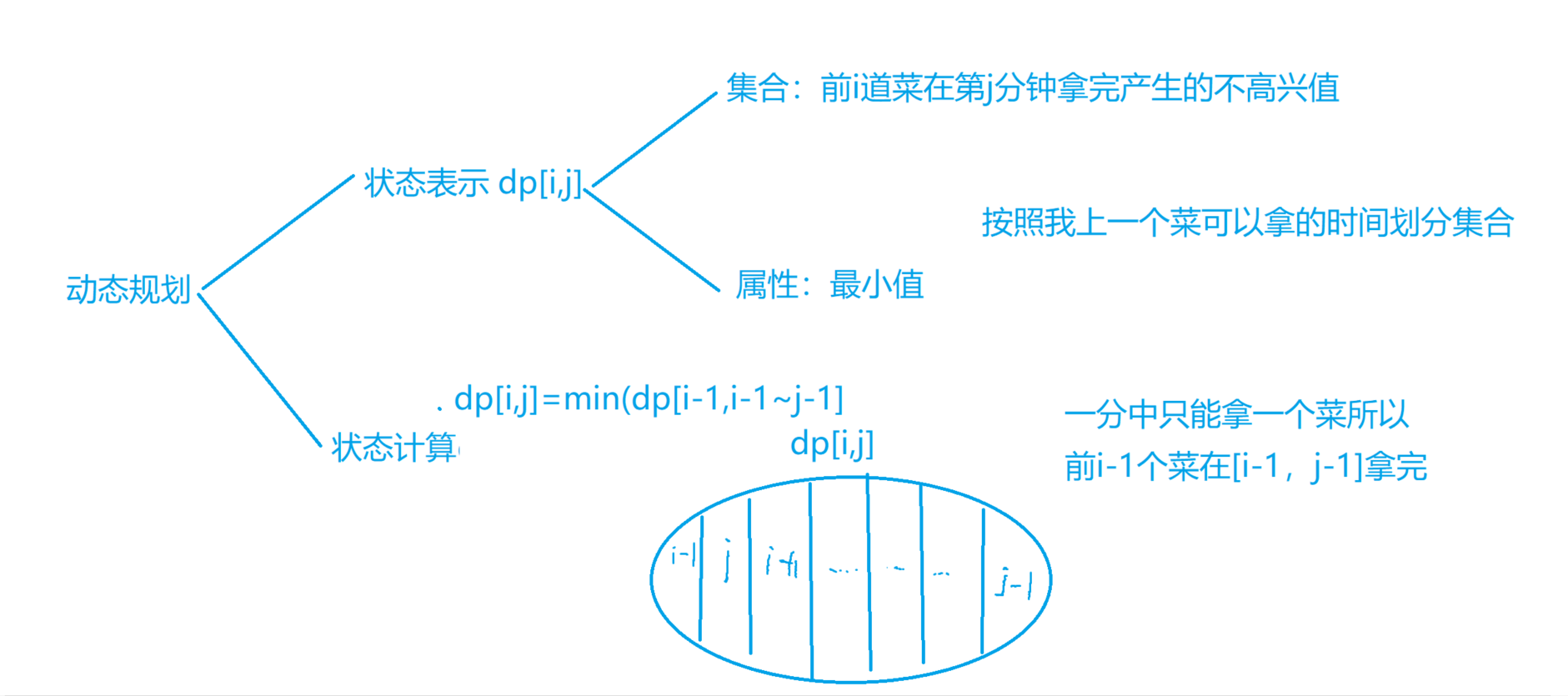
解题思路
吧 每道菜拿出来的时间从小到大排序
初始化dp数组 先初始化成最大值
然后从0到2*n时刻 dp[0][i]=0
接下来dp就完事了

#include<bits/stdc++.h>
const int maxn = 400+10;
using namespace std;
int f[maxn][maxn],m,n,t[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>m;
    while(m--)
    {
        cin>>n;
        memset(f,0x3f,sizeof f);
        for(int i=1;i<=n;i++) cin>>t[i];
        sort(t+1,t+1+n);
        for(int i=0;i<=2*n;i++) f[0][i]=0;//因为要考虑到第一道菜退化成i-1也就是0道菜时间最小值是i-1也就是0所以要初始化第0时刻 
        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=2*n;j++)
            {
                for(int k=i-1;k<=j-1;k++)
                {
                    f[i][j]=min(f[i][j],f[i-1][k]+abs(t[i]-j));
                }
            }
        }
        int ans = 2e9;
        for(int i=n;i<=2*n;i++) ans=min(ans,f[n][i]);
        cout<<ans<<endl;
    }
    return 0;
}