整数划分

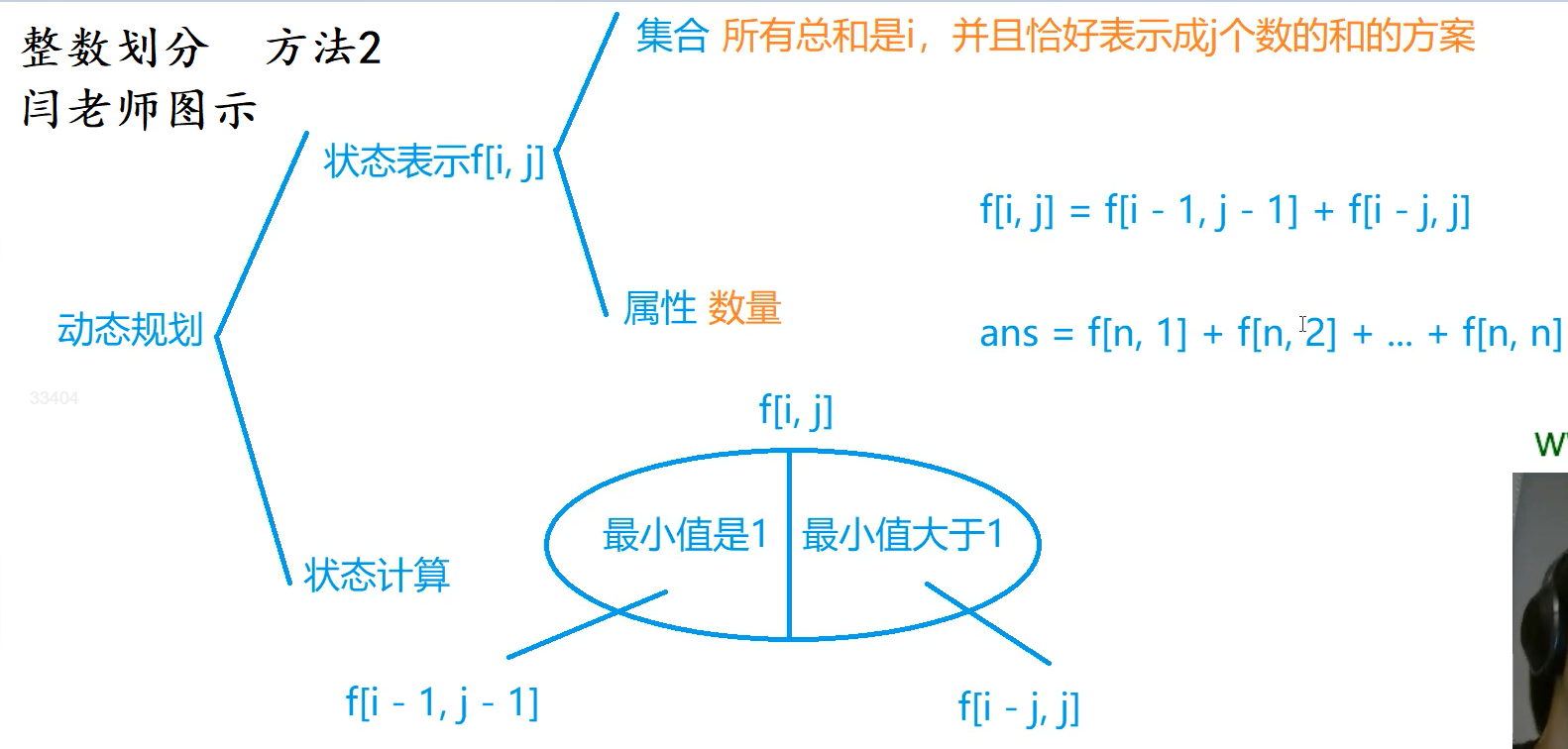
图示（闫老师的上课的截屏，把老师的脸已经切掉了，大家如果想看脸看视频吧

题目描述

一个正整数n可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中n1≥n2≥…≥nk,k≥1。我们将这样的一种表示称为正整数n的一种划分。现在给定一个正整数n，请你求出n共有多少种不同的划分方法。

输入格式

共一行，包含一个整数n。

输出格式

共一行，包含一个整数，表示总划分数量。

由于答案可能很大，输出结果请对109+7取模。

数据范围

1≤n≤1000

样例

输入样例:

5

输出样例：

7

算法1

(暴力枚举) $O(n)$

时间复杂度

$O(n)$

参考文献

C++ 代码

#include<iostream>
#include<algorithm>
using namespace std;
const int mod=1e9+7;
int n,f[1005],i,j;
int main()
{
    scanf("%d",&n);
    f[0]=1;
    for(i=1;i<=n;i++)for(j=i;j<=n;j++)f[j]=(f[j]+f[j-i])%mod;
    printf("%d\n",f[n]);
    return 0;
}

算法2

(暴力枚举) $O(nlogn)$

时间复杂度

$O(nlogn)$

参考文献

无

C++ 代码

#include<iostream>
#include<algorithm>
using namespace std;
const int mod=1e9+7;
int n,f[1005][1005],i,j,ans=0;
int main()
{
    scanf("%d",&n);
    f[0][0]=1;
    for(i=1;i<=n;i++)for(j=1;j<=i;j++)f[i][j]=(f[i-1][j-1]+f[i-j][j])%mod;
    for(i=1;i<=n;i++)ans=(ans+f[n][i])%mod;
    printf("%d\n",ans);
    return 0;
}