开始讲课！

首先我们要知道，这是一道dp题（显而易见）

然后我们通过分析可以知道，这道题可以用前缀和做。

那么现在我们就开始讲题了。

首先我们假设一个n位数，那么我们如何去判断这个数是不是“不降数”呢？

我们先将这个n位数的每一位数抠出来，那么最高位就是a[n-1],第二位是a[n-2]，第三位是a[n-3]……最后一位是a[0]。

然后我们开始分析。首先最高位是a[n-1],那么就将他分成两种情况：0~a[n-1]-1和a[n-1]。如果是第一种情况，那么我们是可以用预处理的方法做出来的（不要问我为什么，dp如此）；如果是第二种的话，那么我们继续划分。那么第二位的数又有两种情况：0~a[n-2]-1和a[n-2]。如果是第一种情况，我们也是能用预处理的方法求出来的；如果是第二种情况，那么我们继续划分……如此下去，直到划分到最后一位。

在所有分类中，所有的第一种情况都是可以通过预处理做出来的。

这里借用一下yxc——闫总大佬的图：

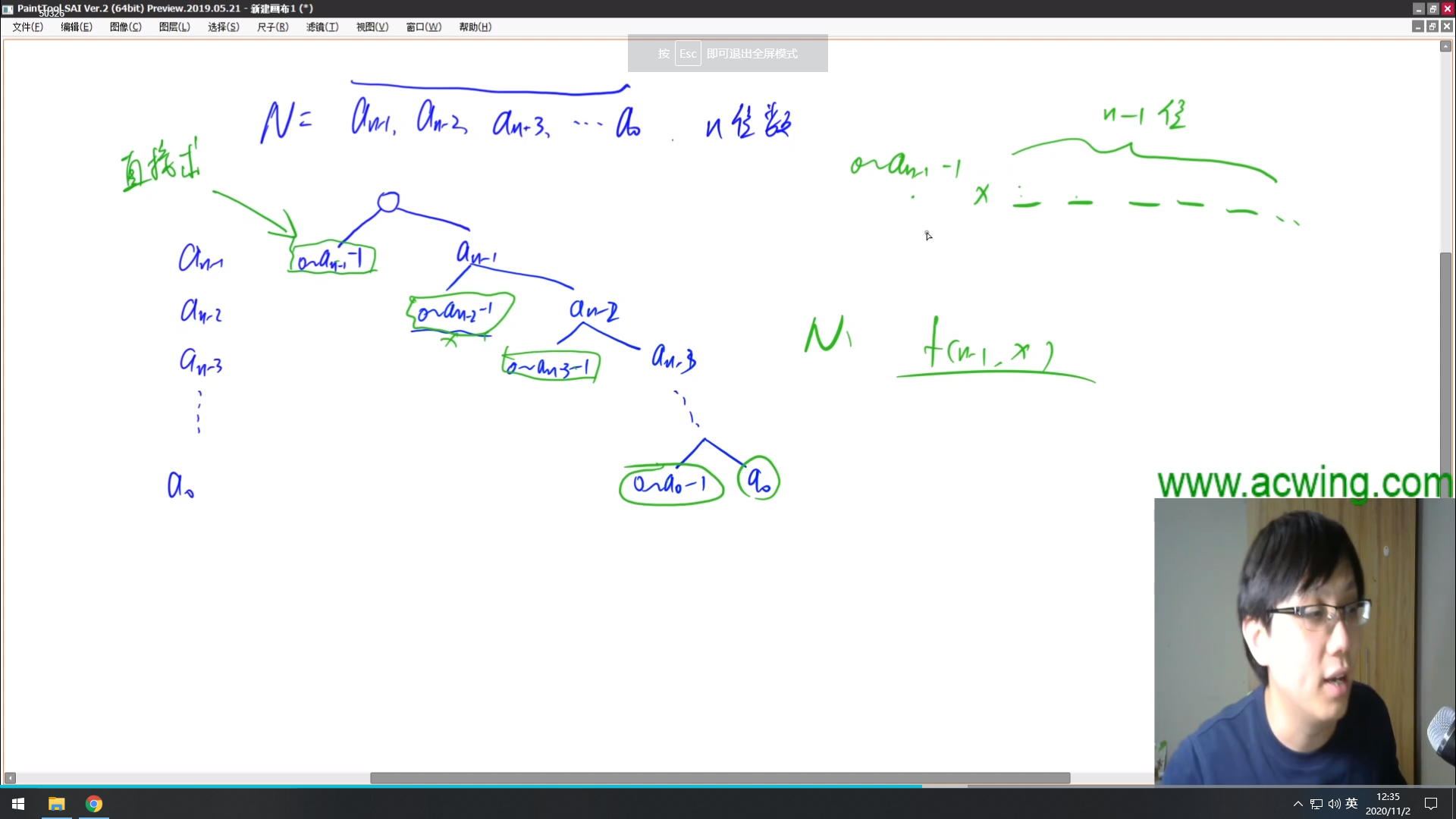
然后我们再来分析一下如何去表示我们的每一个答案。

首先，我们分析一下题目，就可以知道这道题状态表示的集合是所有最高位为j，且一共有i为的不降数的集合，属性是数量。那么我们就可以用f[i,j]表示。那么我们通过比较简单的思索就可以知道，f[i,j]的值就是他的所有子集的和。化成动态转移方程就是：

f[i,j]=f[i-1,j]+f[i-1,j+1]+f[i-1,j+2]+......+f[i-1,9]

那么综合以上两点，就可以阿卡（AK）这道题了！

注释代码时刻

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

//数位DP有很容易辨认的特点。
//在数轴上，求某一区间内满足要求的个数，一般做法是利用前缀和的思想，dp[r]-dp[l-1]；
//每道题的不同之处就是数需要满足的要求，即dp函数的写法。
//一般用树形去分析,dp函数都有last

const int N = 15; // 2的31次方是十位数，建议开为15保险 

int f[N][N];    // f[i, j]表示一共有i位，且最高位填j的数的个数

void init() // 初始化 
{
    for(int i = 0; i <= 9; i ++) f[1][i]=1;


    for (int i = 2; i < N; i ++ )
        for (int j = 0; j <= 9; j ++ )
            for (int k = j; k <= 9; k ++ )
                f[i][j] += f[i - 1][k];
                // f[i,j]=f[i-1,j]+f[i-1,j+1]+f[i-1,j+2]+...+f[i-1,9]
}

int dp(int n)
{
    if (!n) return 1;
    //为了后面没有那么多麻烦，这里要特判。 

    vector<int> nums; // 存储每一个数位上的数 
    while (n) nums.push_back(n % 10), n /= 10; // 数字分解+存储 

    int res = 0; // 定义返回值 
    int last = 0; // 定义上一个数位上的数 
    for (int i = nums.size() - 1; i >= 0; i -- ) // 枚举每一个数位上的数 
    {
        int x = nums[i]; // 特别取出使用 
        for (int j = last; j < x; j ++ ) // 循环 
            res += f[i + 1][j]; // 加上答案 

        if (x < last) break; // 如果不符合“不降数”的要求，退出循环 
        last = x; // 更新 

        if (!i) res ++ ; // 如果顺利循环到底，再加一次 
    }

    return res; // 返回 
}

int main(){
    init(); // 调用初始化函数 

    int l, r;
    while (cin >> l >> r) /*输入多组测试数据*/ cout << dp(r) - dp(l - 1) << endl; // 前缀和 

    return 0;
}