题目描述

给定一个整数序列：a1, a2, ..., an，一个132模式的子序列 ai, aj, ak 被定义为：当 i < j < k 时，ai < ak < aj。设计一个算法，当给定有 n 个数字的序列时，验证这个序列中是否含有132模式的子序列。

注意：n 的值小于15000。

样例

输入: [1, 2, 3, 4]

输出: False

解释: 序列中不存在132模式的子序列。

输入: [3, 1, 4, 2]

输出: True

解释: 序列中有 1 个132模式的子序列： [1, 4, 2].

输入: [-1, 3, 2, 0]

输出: True

解释: 序列中有 3 个132模式的的子序列: [-1, 3, 2], [-1, 3, 0] 和 [-1, 2, 0].

算法分析

单调栈（特殊单调栈）

该题等价于 对于任意一个ai，在后面的元素中是否存在某个组合(aj, ak)，使得ak > aj，其中aj > ak。

从后往前枚举ai，如何快速求出满足要求的ak ?

• 1、用单调递减栈维护在(ai, ak)之间大于ak的数aj，并且从后往前呈现aj值递减的形式，也就是说单调递减栈中的每个元素都大于ak，并且栈顶元素是最小的aj
• 2、使用right记录最大满足要求的数ak（ak尽可能往大的取）

如何维护单调递减栈？如图所示

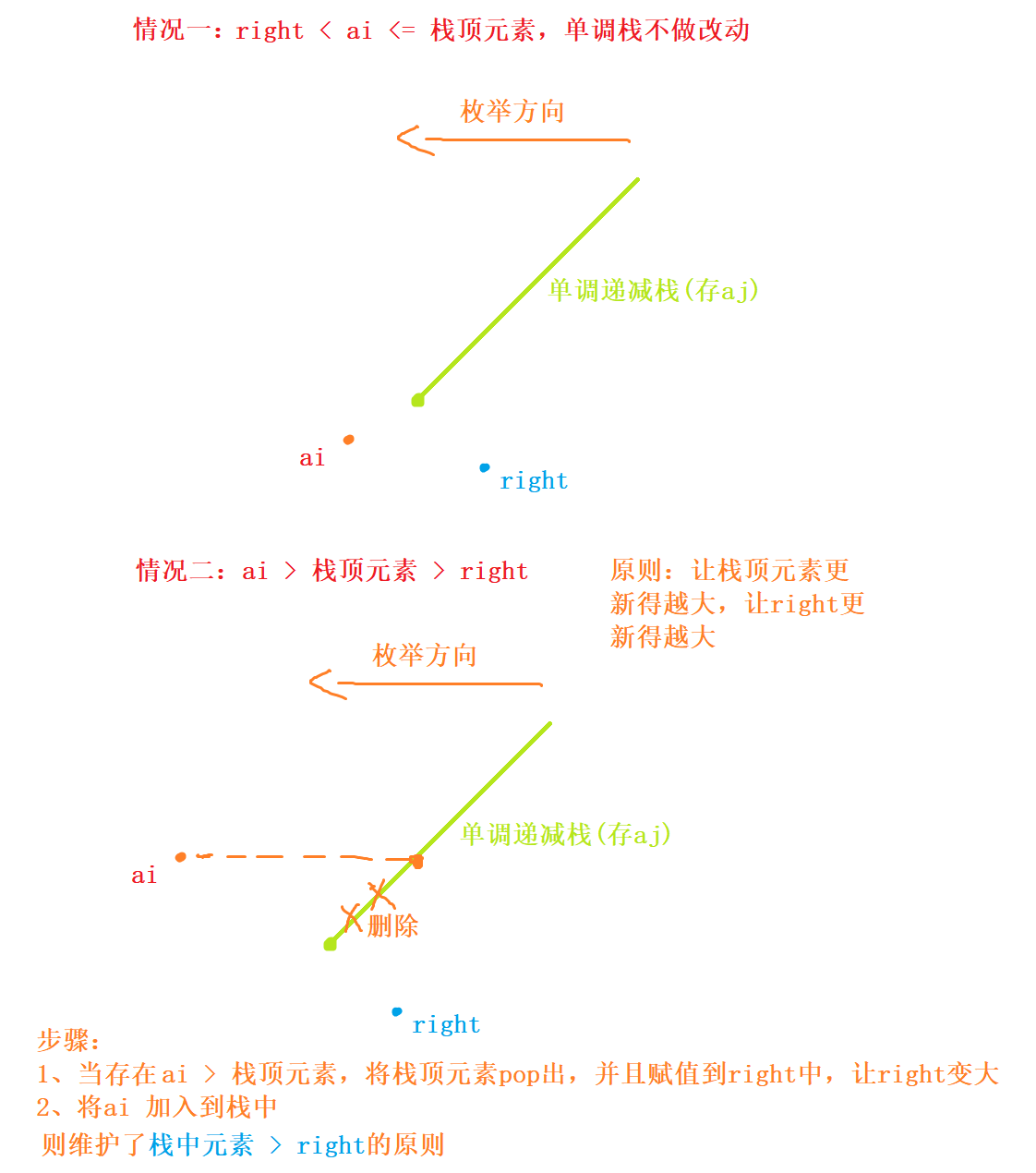
时间复杂度 $O(n)$

Java 代码

class Solution {
    public boolean find132pattern(int[] nums) {
        Stack<Integer> stk = new Stack<Integer>();
        int n = nums.length;
        int right = Integer.MIN_VALUE;
        for(int i = n - 1;i >= 0;i --)
        {
            if(nums[i] < right) return true;
            while(!stk.isEmpty() && nums[i] > stk.peek())
            {
                right = stk.pop();
            } 
            stk.add(nums[i]);
        }
        return false;
    }
}