题目描述

Bob 站在单元格 (0, 0)，想要前往目的地 destination：(row, column)。他只能向 右 或向 下 走。你可以为 Bob 提供导航 指令 来帮助他到达目的地 destination。

指令 用字符串表示，其中每个字符：

• 'H'，意味着水平向右移动
• 'V'，意味着竖直向下移动

能够为 Bob 导航到目的地 destination 的指令可以有多种，例如，如果目的地 destination 是 (2, 3)，"HHHVV" 和 "HVHVH" 都是有效 指令。

然而，Bob 很挑剔。因为他的幸运数字是 k，他想要遵循 按字典序排列后的第 k 条最小指令 的导航前往目的地 destination。k 的编号 从 1 开始。

给定一个整数数组 destination 和一个整数 k，请你返回可以为 Bob 提供前往目的地 destination 导航的 按字典序排列后的第 k 条最小指令。

样例

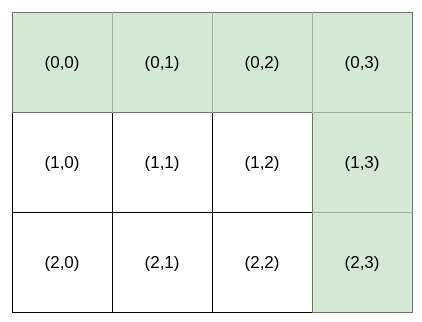
输入：destination = [2,3], k = 1
输出："HHHVV"
解释：能前往 (2, 3) 的所有导航指令 按字典序排列后 如下所示：
["HHHVV", "HHVHV", "HHVVH", "HVHHV", "HVHVH",
 "HVVHH", "VHHHV", "VHHVH", "VHVHH", "VVHHH"]。

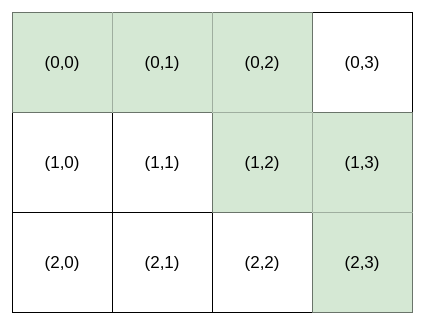
输入：destination = [2,3], k = 2
输出："HHVHV"

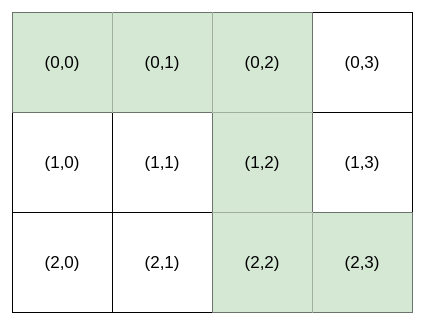
输入：destination = [2,3], k = 3
输出："HHVVH"

限制

• destination.length == 2
• 1 <= row, column <= 15
• 1 <= k <= nCr(row + column, row)，其中 nCr(a, b) 表示组合数，即从 a 个物品中选 b 个物品的不同方案数。

算法

(二叉查询) $O(r + c)$

1. 将 H 看做 0，V 看做 1，题目要求的就是字典序第 k 个 01 串。
2. 从高位开始往低位确定数字
   • 如果 0 的剩余个数为 0，则只能填 1。
   • 否则，计算出这一位如果填 0 后，后续共有多少种可能（通过公式 $ {i - 1} \choose {zero - 1}$ 求出），记为 x
     • 如果 k > x，则说明这一位不应该填 0，需要填 1，同时 k 应该减去 x。
     • 否则，这一位填 0。
3. 可以预处理组合数数组避免整数计算溢出。

时间复杂度

• 共遍历 $r + c$ 次，每一次仅需要判断组合数，故总时间复杂度为 $O(r + c)$。

空间复杂度

• 仅需要 $O(r + c)$ 的空间存储预处理的组合数数组。

C++ 代码

class Solution {
public:
    string kthSmallestPath(vector<int>& destination, int k) {
        int zero = destination[1], one = destination[0];
        const int n = zero + one;
        vector<vector<int>> C(n + 1, vector<int>(n + 1));
        C[0][0] = 1;
        for (int i = 1; i <= zero + one; i++) {
            C[i][0] = 1;
            for (int j = 1; j <= i; j++)
                C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
        }

        string ans;
        for (int i = n; i >= 1; i--) {
            if (zero == 0) ans += "V";
            else {
                if (k > C[i - 1][zero - 1]) {
                    k -= C[i - 1][zero - 1];
                    ans += "V";
                    one--;
                } else {
                    ans += "H";
                    zero--;
                }
            }
        }

        return ans;
    }
};