算法分析

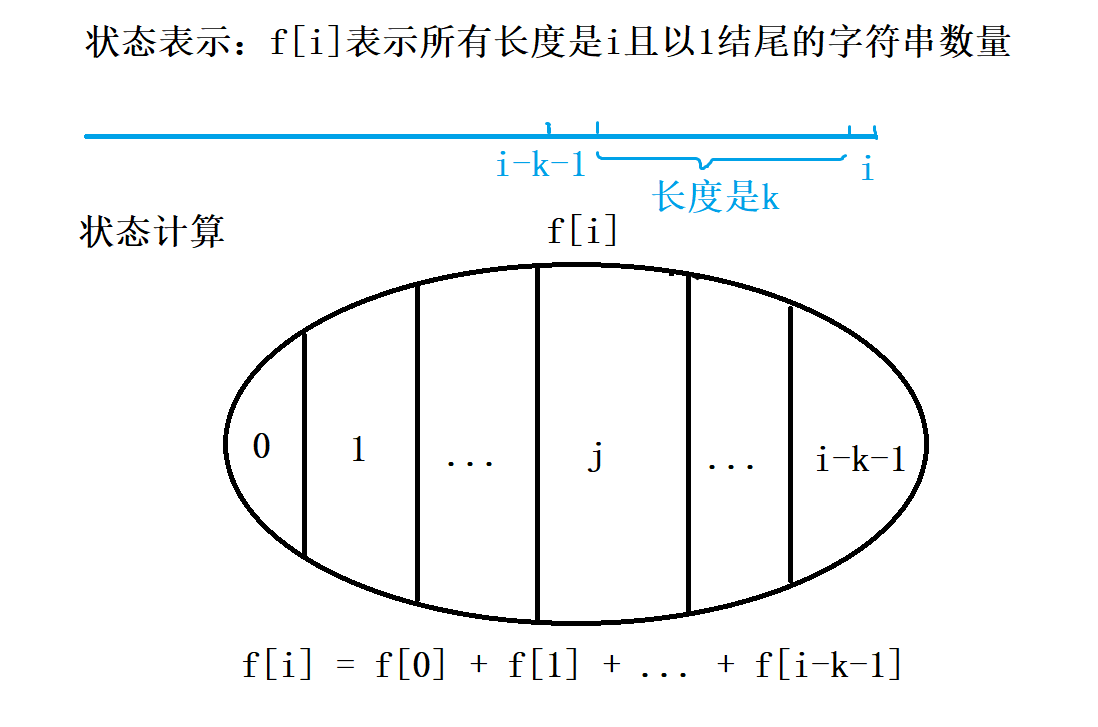
• 初始化：f[0] = 1(f[0]表示不摆放1的情况，初始值这么设，能让整个递归过程的边界是正确的则可行)
• 结果：f[0] + f[1] + f[2] + ... + f[n]

通过s[i]记录f[0] + ... + f[i]的前缀和可以优化到$O(n)$

时间复杂度 $O(n)$

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 100000 + 10, mod = 5000011 ;
    static int[] f = new int[N];
    static int[] s = new int[N];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int k = scan.nextInt();

        f[0] = s[0] = 1;
        for(int i = 1;i <= n;i ++)
        {
            f[i] = s[Math.max(0, i - k - 1)];
            s[i] = (s[i - 1] + f[i]) % mod;
        }
        System.out.println(s[n]);
    }
}