题目分析

本题由于题干过长，可能导致部分同学阅读体验极差，在此简化一下

一个 n×n 大小的矩阵 A，其中每个元素是一个 [0,L) 范围内的整数。

对于矩阵中任意一个元素 A(i,j)（0≤i,j<n），其邻域定义为附近若干元素的集和：

Neighbor(i,j,r)={A(i,j) | 0 ≤ x, y < n and |x − i| ≤ r and |y − j| ≤ r}

这里使用了一个额外的参数 r 来指明 Aij 附近元素的具体范围。

根据定义，易知 Neighbor(i,j,r) 最多有 (2r+1)2 个元素。

如果元素 A(i,j) 邻域中所有元素的平均值小于或等于一个给定的阈值 t，我们就认为该元素处于较暗区域。

现给定邻域参数 r 和阈值 t，试统计该矩阵中有多少元素处于较暗区域。

输入格式

输入共 n+1 行。

输入的第一行包含四个用空格分隔的正整数 n、L、r 和 t，含义如前文所述。

第二到第 n+1 行输入矩阵 A。第 i+2（0≤i<n）行包含用空格分隔的 n 个整数，依次为 Ai0,Ai1,⋯,Ai(n−1)。

输出格式

输出一个整数，表示输入灰度图像中处于较暗区域的像素总数。

数据范围

70% 的测试数据满足 n≤100、r≤10。

全部的测试数据满足 0<n≤600、0<r≤100 且 2≤t<L≤256。

输入样例：

4 16 1 6
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

输出样例：

7

思路

采用前缀和，得出s[N][N]。

然后对每一个元素的邻域进行检查，以下为对s[1][2]和s[3][3]的检查。（偷懒，直接拿s数组了

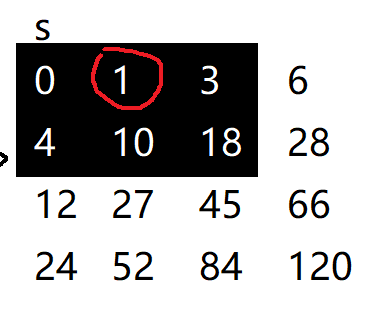
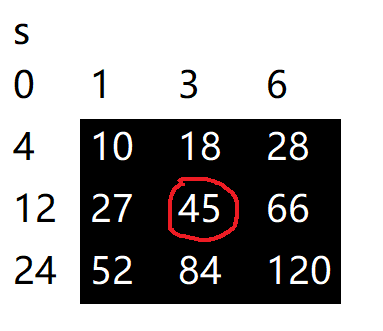
直接利用前缀和解得该区域的和，然后得出该区域有几个元素，两者相除再与t作比较即可解出。

c++代码

#include<iostream>
using namespace std;
const int N = 610;
int a[N][N];
int n, l, r, t;
int main()
{
    int res = 0; // 保存结果
    cin >> n >> l >> r >> t ;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++) 
        {
            int x;
            cin >> x;
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + x; // 输入元素值，并得出前缀和
        }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)//遍历检查
        {
            int s, m;
            int x1, y1, x2, y2;//得出区域的右下角和左上角
            x1 = max(1, i - r);
            y1 = max(1, j - r);
            x2 = min(n, i + r);
            y2 = min(n, j + r);
            s = a[x2][y2] - a[x1 - 1][y2] - a[x2][y1 - 1] + a[x1 - 1][y1 - 1];//直接前缀和算
            m = (y2 - y1 + 1) * (x2 - x1 + 1); //元素数量
            if(s <= t * m) res ++; //判断是否小于等于t
        }
    cout << res;    
}