题目描述

给定一棵二叉树的根 root，请你考虑它所有从根到叶的路径：从根到任何叶的路径。（所谓一个叶子节点，就是一个没有子节点的节点。）

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点，需要被删除。

请你删除所有不足节点，并返回生成的二叉树的根。

样例

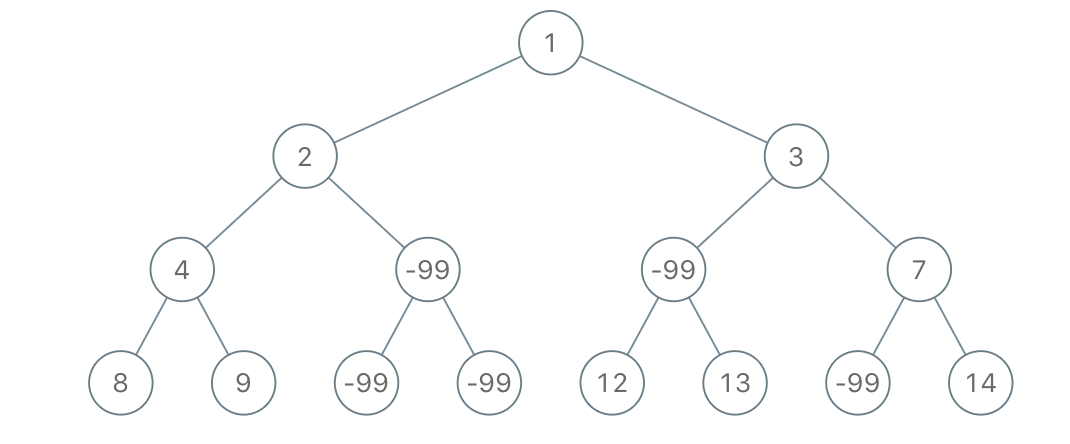
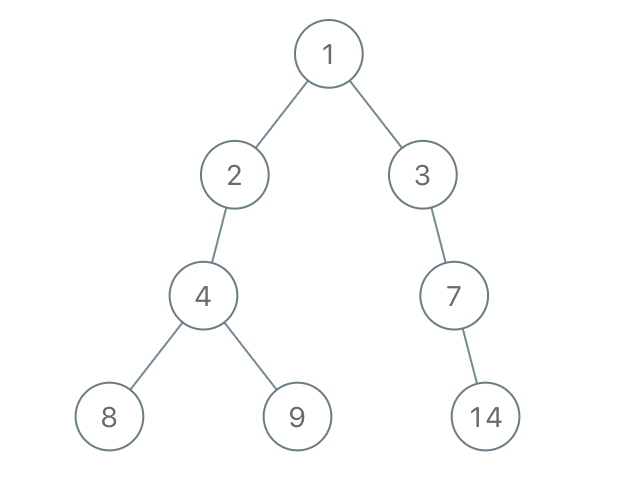
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

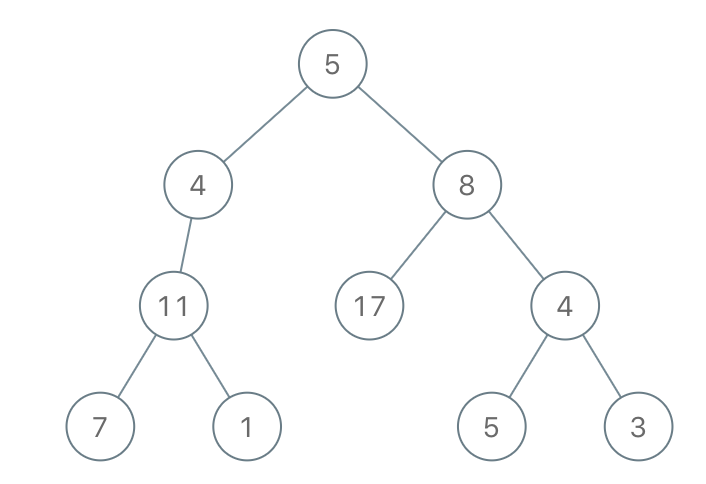
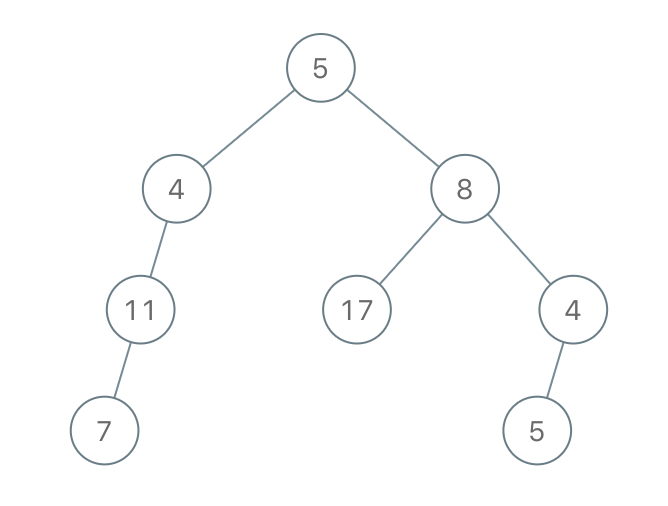
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

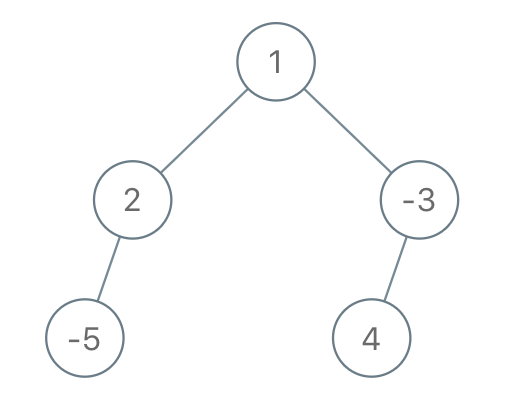
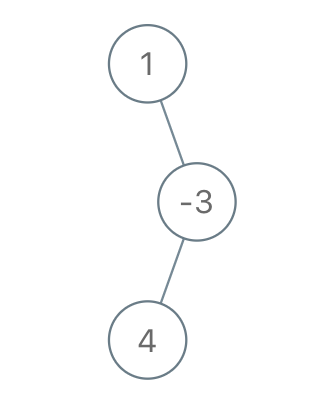
输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

注意

• 给定的树有 1 到 5000 个结点。
• -10^5 <= node.val <= 10^5
• -10^9 <= limit <= 10^9

算法

(递归) $O(n)$

1. 采用自底向上的删除策略。
2. 如果某个结点是叶子结点，则判断到根结点的路径是否小于 limit。如果小于，则直接将其变为 NULL，然后回溯。
3. 如果不是叶子结点，则递归删除左儿子结点和（或）右儿子结点。如果当前结点变为了叶子结点，也将其变为 NULL，因为这代表着所有 “根-叶” 路径都小于 limit。

时间复杂度

• 每个结点遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 递归需要栈空间，故空间复杂度为 $O(h)$，$h$ 为树的最大高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void cut(TreeNode* &root, int limit, int sum) {
        if (root -> left == NULL && root -> right == NULL) {
            if (sum < limit)
                root = NULL;
            return;
        }
        if (root -> left) {
            cut(root -> left, limit, sum + root -> left -> val);
        }
        if (root -> right) {
            cut(root -> right, limit, sum + root -> right -> val);
        }
        if (root -> left == NULL && root -> right == NULL)
            root = NULL;
    }


    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        cut(root, limit, root -> val);
        return root;
    }
};