题目描述

给你一个整数 n 和一个二维整数数组 queries。

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（0 <= i < n - 1）。

queries[i] = [u_i, v_i] 表示新建一条从城市 u_i 到城市 v_i 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的 长度。

样例

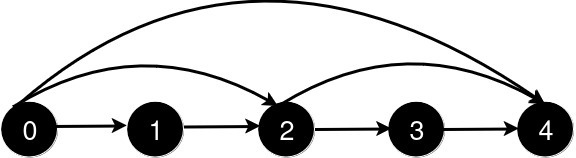
输入： n = 5, queries = [[2, 4], [0, 2], [0, 4]]

输出： [3, 2, 1]

解释：

新增一条从 2 到 4 的道路后，从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后，从 0 到 4 的最短路径长度为 2。

新增一条从 0 到 4 的道路后，从 0 到 4 的最短路径长度为 1。

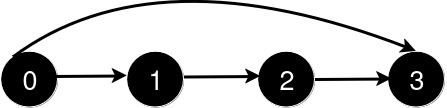
输入： n = 4, queries = [[0, 3], [0, 2]]

输出： [1, 1]

解释：

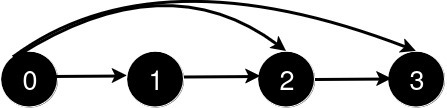
新增一条从 0 到 3 的道路后，从 0 到 3 的最短路径长度为 1。

新增一条从 0 到 2 的道路后，从 0 到 3 的最短路径长度仍为 1。

限制

• 3 <= n <= 10^5
• 1 <= queries.length <= 10^5
• queries[i].length == 2
• 0 <= queries[i][0] < queries[i][1] < n
• 1 < queries[i][1] - queries[i][0]
• 查询中没有重复的道路。
• 不存在两个查询都满足 i != j 且 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

算法1

(线段树) $O(n + m \log n)$

1. 将 $n$ 个端点转为 $n-1$ 条线段。每次操作没有相交的线段，只存在完全包含或者完全互斥的线段。
2. 每次操作相当于合并若干条线段，如果线段已经被合并，则无需再次合并。每次查询相当于求解当前线段的数量。
3. 使用线段树记录区间和。初始时，每个线段的值为 $1$。每次操作合并时，如果将当前区间内的线段合并为一条，仅在区间起点的线段值记为 $1$，其余的值都记为 $0$。合并前，如果发现待合并线段的权重小于等于 $1$，则证明这个线段已经被合并过了，无需再次合并。
4. 查询的答案就是线段树根节点的值。

时间复杂度

• 初始化线段树的时间复杂度为 $O(n)$。
• 每次操作和查询的时间复杂度为 $O(\log n)$。
• 故总时间复杂度为 $O(n + m \log n)$，$m$ 为总的操作次数。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储线段树和答案。

C++ 代码

const int N = 100010;

class Solution {
private:
    int sum[N << 2], mark[N << 2];

    void pushdown(int rt, int len) {
        if (mark[rt] == -1)
            return;

        sum[rt << 1] = mark[rt] * (len - (len >> 1));
        sum[rt << 1 | 1] = mark[rt] * (len >> 1);
        mark[rt << 1] = mark[rt << 1 | 1] = mark[rt];
        mark[rt] = -1;
    }

    void build(int l, int r, int rt) {
        if (l == r) {
            sum[rt] = 1;
            return;
        }

        int mid = (l + r) >> 1;
        build(l, mid, rt << 1);
        build(mid + 1, r, rt << 1 | 1);

        sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
        mark[rt] = -1;
    }

    int query(int L, int R, int l, int r, int rt) {
        if (L <= l && r <= R)
            return sum[rt];

        pushdown(rt, r - l + 1);

        int mid = (l + r) >> 1, res = 0;
        if (L <= mid) res += query(L, R, l, mid, rt << 1);
        if (mid < R) res += query(L, R, mid + 1, r, rt << 1 | 1);

        return res;
    }

    void update(int L, int R, int x, int l, int r, int rt) {
        if (L <= l && r <= R) {
            sum[rt] = x * (r - l + 1);
            mark[rt] = x;
            return;
        }

        pushdown(rt, r - l + 1);

        int mid = (l + r) >> 1;
        if (L <= mid) update(L, R, x, l, mid, rt << 1);
        if (mid < R) update(L, R, x, mid + 1, r, rt << 1 | 1);

        sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
    }

public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        build(1, n - 1, 1);

        const int m = queries.size();
        vector<int> ans(m);

        for (int i = 0; i < m; i++) {
            int L = queries[i][0] + 1, R = queries[i][1];
            if (query(L, R, 1, n - 1, 1) > 1) {
                update(L, L, 1, 1, n - 1, 1);
                update(L + 1, R, 0, 1, n - 1, 1);
            }

            ans[i] = sum[1]
        }

        return ans;
    }
};

算法2

(有序集) $O((n + m) \log n)$

1. 根据算法 1 的思路，用 C++ 中的有序集直接维护线段。
2. 初始时，将 $[0, 1],[1, 2],\dots, [n - 2, n - 1]$ 这 $n-1$ 条线段插入到有序集中。
3. 对于每次操作的线段 $[L, R]$，在有序集中查询线段起点大于等于 $L$ 的线段，如果有查询到且被查询到的线段起点小于 $R$，则删除这个线段。
4. 如果上述步骤中有删除线段，则将 $[L, R]$ 插入到有序集中。
5. 每次查询的答案就是有序集的大小。

时间复杂度

• 初始化的时间复杂度为 $O(n \log n)$。
• 对于每条线段，最多被插入一次，删除一次，单次操作的时间复杂度都是 $O(\log n)$。
• 故总时间复杂度为 $O((n + m) \log n)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储有序集和答案。

C++ 代码

class Solution {
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        set<pair<int, int>> s;

        for (int i = 1; i < n; i++)
            s.insert(make_pair(i - 1, i));

        const int m = queries.size();
        vector<int> ans(m);

        for (int i = 0; i < m; i++) {
            int L = queries[i][0], R = queries[i][1];
            bool found = false;

            while (1) {
                auto it = s.upper_bound(make_pair(L, -1));
                if (it == s.end() || it->first >= R)
                    break;

                s.erase(it);
                found = true;
            }

            if (found)
                s.insert(make_pair(L, R));

            ans[i] = s.size();
        }

        return ans;
    }
};