题目描述

样例

输入

5 3 1
3 2 5 2 3

输出

4

思路：

(前缀和+二分) $O(nlogn)$

看到n的范围想到只能控制在$O(nlogn)$以内，而题意说是从前x个人中任意选择k个人的成绩，并且答案求的是至少要检查多少个人的成绩才能满足要求，这让我们不妨想到如果从前个x人中选k个人不满足要求，那么x-1也一定不满足，因为如果x-1满足，那么在前x个人中我同样可以选择前x-1中那个答案。同理如果x满足，那么x+1也必然满足。如此分析而来，我们在找答案时该序列满足二段性，可以用二分 $O(logn)$来找。

然后就是check函数，我们必须控制在$O(n)$，由题意我们知道我们要求的是前x个成绩中有没有k个成绩组合的方差小于t，而方差反映的是数的紧凑程度，彼此之间的差值越小，方差越小，于是我们可以将前x个数排序，再以k个数为单位遍历，如此求出来的每一个方差必定是所有组合中最小的，若如此不符合要求，那么前x个数中便无解。而题意给的方差公式比较难以用$O(n)$的方法实现，我们展开的话：

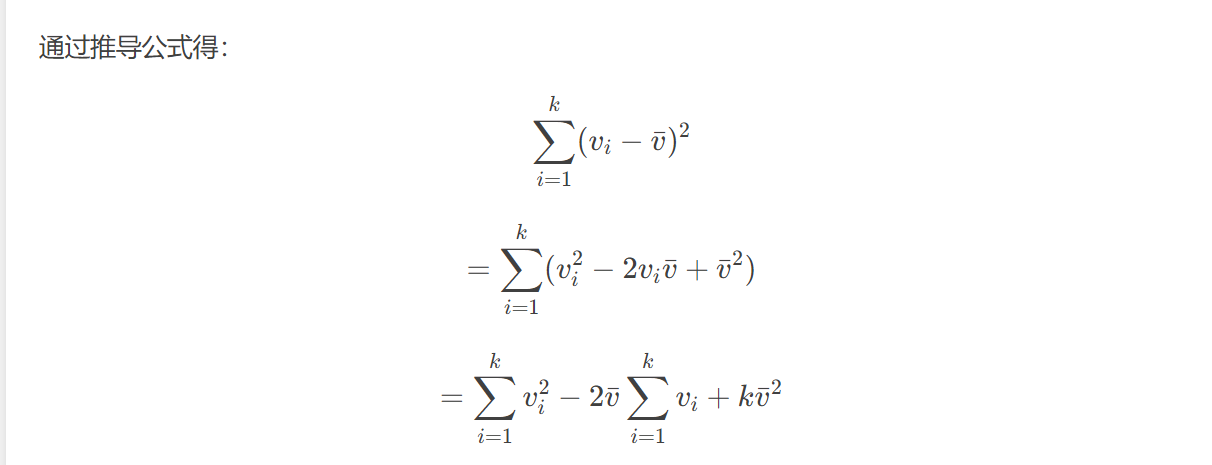
用前缀和加上滑动窗口即可在$O(n)$求出k个数的平方和

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=100010;
typedef long long LL;
int n,k,t;
int a[N],b[N];
LL s1[N],s2[N];

bool check(int x)
{
    memcpy(b,a,sizeof a);//将数组复制给a，因为下一次check还要用原数组
    //注意排序是1~下,而不是1~n;否则如果x之后有更小的数据会影响
    sort(b+1,b+x+1);
    //处理前k个数的和与平方和
    for(int i=1;i<=x;i++)
    {
        s1[i]=s1[i-1]+b[i];//和
        s2[i]=s2[i-1]+(LL)b[i]*b[i];//平方和
    }
    //滑动窗口
    for (int i = k; i <= x; i ++){
        //维护一个窗口大小为k的和
        LL spowvi = s2[i] - s2[i - k], svi = s1[i] - s1[i - k];
        double avg = (double)svi / k;
        if ((double)spowvi - avg * 2 * svi + k * avg * avg < (double)k * t) return true;
    }
    return false;
}

int main()
{
    cin>>n>>k>>t;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    //如果已经统计过所有人成绩还是无法得出答案则无解
    if(!check(n)) cout<<"-1";
    else
    {
        int l=k,r=n;
        while(l<r)
        {
            int mid=l+r>>1;
            if(check(mid)) r=mid;
            else l=mid+1;
        }
        cout<<l;
    }
    return 0;
}