区间选点

题目描述

 给定 N 个闭区间 [ai,bi]

，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。
输入格式

第一行包含整数 N

，表示区间数。

接下来 N
行，每行包含两个整数 ai,bi

，表示一个区间的两个端点。
输出格式

输出一个整数，表示所需的点的最小数量。
数据范围

1≤N≤105
,
−109≤ai≤bi≤109

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

这题是使用贪心来写的。
首先我们分析下题目要我们干什么。

给定 N 个闭区间 [ai,bi]

，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

要我们选择尽量少的点，使所有的区间都包含这个点。
我们可以发现，每个点选的位置都必须在每个区间重合的位置。

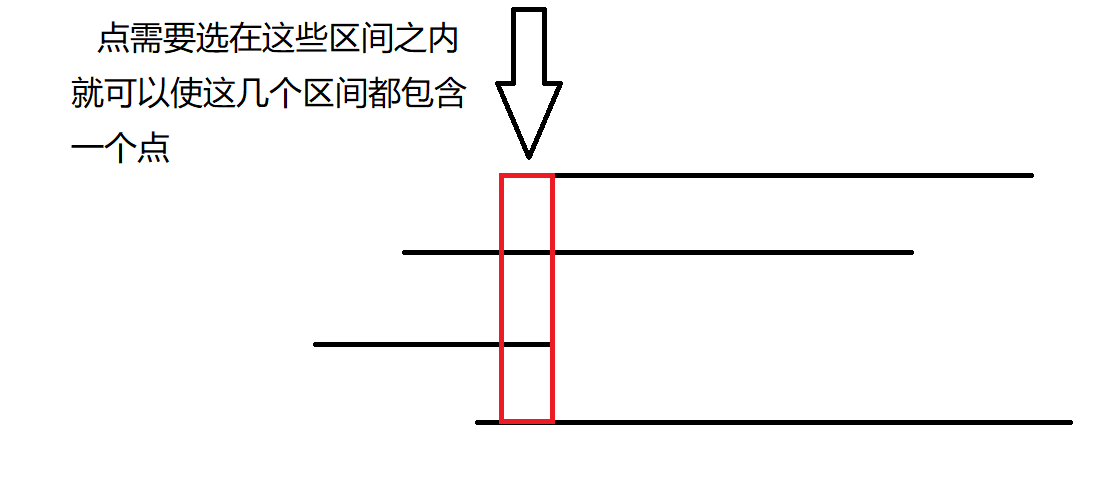
那怎么求哪几个区间重合了呢？

我们通过图发现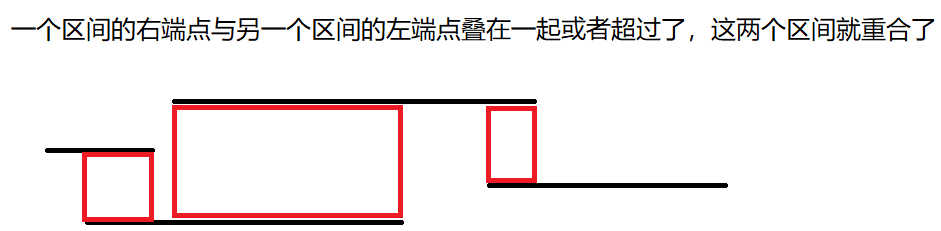
这样通过右端点排序，就可以求出需要多少个点了

代码

#include <bits/stdc++.h>
using namespace std;
struct node{
    int l,r;
}a[100005];
int n;
bool cmp(node a,node b){
    return a.r < b.r;
}//按照左端点排序
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i].l >> a[i].r;
    int res = 0;
    sort(a + 1,a + n + 1,cmp);
    int ed = -2e9;
    for(int i = 1; i <= n; i ++){
        if(a[i].l > ed){//如果这两个区间不重合
            ed = a[i].r;//重新设置新的右端点
            res ++;//点数增加
        }
    }
    cout << res << endl;
    return 0;
}