一、没有上司的舞会

1、解析

• 题意：在一棵树中，父节点与其直接子节点不能同时选择，也即父节点参会直接子节点不能参会，父节点未参会直接子节点可参会
• 状态表示：f[i][st]表示对于根节点为i，状态为st(1选0不选)的树的所有方案
• 状态转移：
  f[i][1] += f[j][0]
  f[i][0] += max(f[j][0], f[j][1])
• 提醒：本题对于Python直接使用dfs会Segmentation Fault，需要用BFS

2、代码

import sys
from collections import defaultdict
sys.setrecursionlimit(100000)
input = lambda: sys.stdin.readline().strip()

n = int(input())
lines = sys.stdin.readlines()
a = [0] + list(map(lambda x: int(x.strip()), lines[:n]))
h = defaultdict(list)
st = [False] * (n + 1)
for x in lines[n: ]:
    l, k = map(lambda x: int(x.strip()), list(x.strip().split()))
    h[k].append(l)
    st[l] = True

root = 1
while st[root]:
    root += 1 
f = [[0, 0] for _ in range(n + 1)]

def dfs(u):
    f[u][1] = a[u]

    for v in h[u]:
        dfs(v)

        f[u][0] += max(f[v][0], f[v][1])
        f[u][1] += f[v][0]
    return

dfs(root)
print(max(f[root][0], f[root][1]))

二、 树的最长路径

1、解析

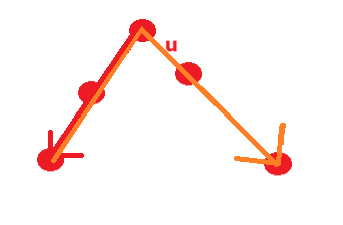
对于经过任意一个点u的最长路径，要么是红色的线，要么是黄色的线
红色：相当于以此为根节点，寻找其最远的子节点
黄色：相当于以此为根节点，寻找最远和次远的子节点

2、代码

import sys
from collections import defaultdict
input = lambda: sys.stdin.readline().strip()

n = int(input())
h = defaultdict(list)
ans = 0
for _ in range(n - 1):
    a, b, c = map(int, input().split())
    h[a].append((b, c))
    h[b].append((a, c))

def dfs(u, root):
    global ans
    Max, SMax = 0, 0
    for v, w in h[u]:
        if v == root: continue
        dis = dfs(v, u) + w

        if dis > Max:
            SMax = Max
            Max = dis
        elif dis > SMax:
            SMax =  dis

    ans = max(ans, Max + SMax)
    return Max 

dfs(1, -1)
print(ans)

三、 树的中心

1、解析

对于任意一个点u，其到所有点的最远距离要么向下，要么向上
向下：u到其最远子节点的距离 -》 依赖于子节点
向上：u的根节点的最远距离是否经过u -》 依赖于父节点
* 是：max(根节点向下的次远距离，根节点向上的距离) + w
* 否：max(根节点向下的最远距离，根节点向上的距离) + w

2、代码

import sys
from collections import defaultdict
sys.setrecursionlimit(100000)

input = lambda: sys.stdin.readline().strip()
n = int(input())
h, down, sdown, up, path = defaultdict(list), [0] * (n + 1), [0] * (n + 1), [0] * (n + 1), [0] * (n + 1)
for _ in range(n - 1):
    a, b, c = map(int, input().split())
    h[a].append((b, c))
    h[b].append((a, c))

def dfs_down(u, root):
    for v, w in h[u]:
        if v == root: continue
        dfs_down(v, u)
        dis = down[v] + w

        if dis > down[u]:
            sdown[u] = down[u]
            down[u] = dis
            path[u] = v
        elif dis > sdown[u]:
            sdown[u] = dis

def dfs_up(u, root):
    for v, w in h[u]:
        if v == root: continue
        up[v] = (max(up[u], sdown[u]) if path[u] == v else max(up[u], down[u])) + w
        dfs_up(v, u)

dfs_down(1, -1)
dfs_up(1, -1)
print(min(max(down[i], up[i]) for i in range(1, n + 1)))

四、 数字转换

1、解析

• 题意：每个数字x可以与其约数之和sum（不包含x）相互转换，但要求sum < x
• 很明显每个数的约数之和唯一，可以唯一地构建一棵树，边为(sum, x)
• 如此一来，转换的最多次数即为树的直径

2、代码

import sys
from collections import defaultdict
sys.setrecursionlimit(1000000)

n = int(input())
sums, h = defaultdict(int), defaultdict(list)
ans = 0

for i in range(1, n + 1):
    j = 2
    while j <= n / i:
        sums[i * j] = sums[i * j] + i
        j += 1
for x in sums:
    if sums[x] < x:
        h[sums[x]].append(x)

def dfs(u):
    global ans
    Max, SMax = 0, 0
    for v in h[u]:
        dis = dfs(v) + 1
        if dis > Max:
            SMax, Max = Max, dis
        elif dis > SMax:
            SMax = dis
    ans = max(ans, Max + SMax)
    return Max

dfs(1)
print(ans)

五、 二叉苹果树

1、解析 – 依赖背包

2、代码

六、 战略游戏

1、解析

• 此题可类比没有上司的舞会，区别在于选择最少点覆盖所有边为此题关键点
• 状态表示：f[u][st]以u为根、状态为st的树的点选择方案

2、代码

import sys
from collections import defaultdict
sys.setrecursionlimit(1000000)

n, h, f = None, None, None
lines = sys.stdin.readlines()
i, j = 0, 0

def dfs(u):
    f[u][1] = 1
    for v in h[u]:
        dfs(v)

        f[u][0] += f[v][1]
        f[u][1] += min(f[v][0], f[v][1])

while i < len(lines):
    n = int(lines[i].strip())
    h, f = defaultdict(list), [[0, 0] for _ in range(n + 1)]
    st, root = [False] * (n + 1), 0

    j = i + 1
    while j <= i + n:
        data = list(map(str, lines[j].strip().split()))
        pos = data[0].find(':')
        u = int(data[0][: pos])
        for v in data[1: ]:
            h[u].append(int(v))
            st[int(v)] = True
        j += 1
    i = j

    while st[root]:
        root += 1

    dfs(root)
    print(min(f[root][0], f[root][1]))

七、 皇宫看守

1、解析

• 与战略游戏的区别：覆盖所有的点不一定需要覆盖所有边
• 根据点u被看守的三种情况划分，f[u][st]
  • f[u][0]（由父节点看守）：u的子节点可以由其子节点或自己看守
  • f[u][2]（由自己看守）：u的子节点可能是任意一种情况
  • f[u][1]（由子节点看守）：假设看守u的点是v，则v的情况一定是自己看守，其余点则可能是有各自的子节点或自己看守
• 答案：根节点一定不会是被其父节点看守，答案只能是min(f[root][1], f[root][2])

2、代码

import sys
from collections import defaultdict
sys.setrecursionlimit(1000000)

input = lambda: sys.stdin.readline().strip()
n = int(input())
h, w, st, root = defaultdict(list), [0] * (n + 1), [False] * (n + 1), 1
f = [[0x3f3f3f3f, 0x3f3f3f3f, 0x3f3f3f3f] for _ in range(n + 1)] # 0父节点看守，1子节点看守，2自己看守
for _ in range(n):
    line = list(map(int, input().split()))
    u, w[u], m = line[: 3]
    for v in line[3: ]:
        h[u].append(v)
        st[v] = True

while st[root]:
    root += 1

def dfs(u):
    f[u][0], f[u][1], f[u][2] = 0, 0x3f3f3f3f, w[u]
    for v in h[u]:
        dfs(v)

        f[u][0] += min(f[v][1], f[v][2])
        f[u][2] += min(f[v][0], f[v][1], f[v][2])

    for v in h[u]:
        f[u][1] = min(f[u][1], f[v][2] + f[u][0] - min(f[v][1], f[v][2]))

dfs(root)
print(min(f[root][1: ]))