题目描述

你正在维护一个项目，该项目有 n 个方法，编号从 0 到 n - 1。

给你两个整数 n 和 k，以及一个二维整数数组 invocations，其中 invocations[i] = [a_i, b_i] 表示方法 a_i 调用了方法 b_i。

已知如果方法 k 存在一个已知的 bug。那么方法 k 以及它直接或间接调用的任何方法都被视为 可疑方法，我们需要从项目中移除这些方法。

只有当一组方法没有被这组之外的任何方法调用时，这组方法才能被移除。

返回一个数组，包含移除所有 可疑方法 后剩下的所有方法。你可以以任意顺序返回答案。如果无法移除 所有 可疑方法，则 不 移除任何方法。

样例

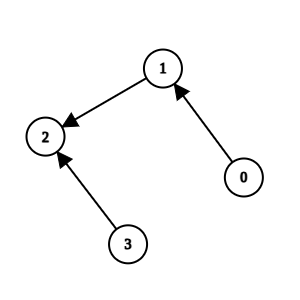
输入：n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]

输出：[0,1,2,3]

解释：

方法 2 和方法 1 是可疑方法，但它们分别直接被方法 3 和方法 0 调用。
由于方法 3 和方法 0 不是可疑方法，我们无法移除任何方法，故返回所有方法。

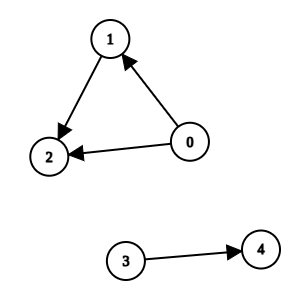
输入：n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]

输出：[3,4]

解释：

方法 0、方法 1 和方法 2 是可疑方法，且没有被任何其他方法直接调用。我们可以移除它们。

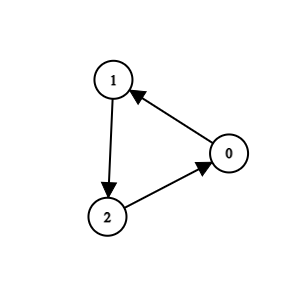
输入：n = 3, k = 2, invocations = [[1,2],[0,1],[2,0]]

输出：[]

解释：

所有方法都是可疑方法。我们可以移除它们。

限制

• 1 <= n <= 10^5
• 0 <= k <= n - 1
• 0 <= invocations.length <= 2 * 10^5
• invocations[i] == [a_i, b_i]
• 0 <= a_i, b_i <= n - 1
• a_i != b_i
• invocations[i] != invocations[j]

算法

(宽度优先遍历) $O(n + m)$

1. 通过宽度优先遍历标记所有可疑的方法。
2. 遍历所有的边，如果存在一条边的起点是不可疑的方法，但终点是可疑的方法，则无法删除。
3. 否则，删除所有被标记的节点。

时间复杂度

• 宽度优先遍历的时间复杂度为 $O(n + m)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储邻接表，宽度优先遍历的队列和答案。

C++ 代码

class Solution {
public:
    vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations) {
        vector<vector<int>> graph(n);

        for (const auto &e : invocations)
            graph[e[0]].push_back(e[1]);

        vector<bool> seen(n, false);
        seen[k] = true;

        queue<int> q;
        q.push(k);

        while (!q.empty()) {
            int u = q.front();
            q.pop();

            for (int v : graph[u]) {
                if (seen[v])
                    continue;

                seen[v] = true;
                q.push(v);
            }
        }

        for (const auto &e : invocations)
            if (!seen[e[0]] && seen[e[1]]) {
                vector<int> ans(n);
                iota(ans.begin(), ans.end(), 0);

                return ans;
            }

        vector<int> ans;
        for (int i = 0; i < n; i++)
            if (!seen[i])
                ans.push_back(i);

        return ans;
    }
};