题目描述

给你一个二维整数数组 edges，它表示一棵 n 个节点的 无向 图，其中 edges[i] = [u_i, v_i] 表示节点 u_i 和 v_i 之间有一条边。

请你构造一个二维矩阵，满足以下条件：

• 矩阵中每个格子 一一对应 图中 0 到 n - 1 的所有节点。
• 矩阵中两个格子相邻（横 的或者 竖 的）当且仅当 它们对应的节点在 edges 中有边连接。

题目保证 edges 可以构造一个满足上述条件的二维矩阵。

请你返回一个符合上述要求的二维整数数组，如果存在多种答案，返回任意一个。

样例

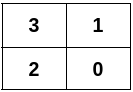
输入：n = 4, edges = [[0,1],[0,2],[1,3],[2,3]]

输出：[[3,1],[2,0]]

解释：

输入：n = 5, edges = [[0,1],[1,3],[2,3],[2,4]]

输出：[[4,2,3,1,0]]

解释：

输入：

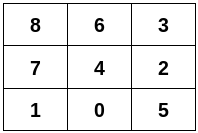
n = 9
edges = [[0,1],[0,4],[0,5],[1,7],[2,3],[2,4],[2,5],[3,6],[4,6],[4,7],[6,8],[7,8]]

输出：[[8,6,3],[7,4,2],[1,0,5]]

解释：

限制

• 2 <= n <= 5 * 10^4
• 1 <= edges.length <= 10^5
• edges[i] = [u_i, v_i]
• 0 <= u_i < v_i < n
• 图中的边互不相同。
• 输入保证 edges 可以形成一个符合上述条件的二维矩阵。

算法

(思维题，模拟) $O(n + m)$

1. 可以通过解二元二次方程组求出最终矩阵的长和宽，假设行数 $r$ 小于等于列数 $c$。
2. 如果 $r = 1$，则直接找到度为 $1$ 的点放到 $(0, 0)$，然后按照关联关系填充。
3. 如果 $r = 2$，则固定两行，找到度为 $2$ 的点 $st$ 放到 $(0, 0)$，然后再将与 $st$ 关联的，度为 $2$ 的点放到 $(1, 0)$，然后按照关联关系填充。
4. 其他情况下，也是找到度为 $2$ 的点放到 $(0, 0)$，然后按照类似的思路填充第一行，即找与上一个点关联点中，度为 $3$ 或者 $2$ 的点作为下一个点。如果找到了度为 $2$ 的点，则说明第一行到达了末尾。（注意，此时不能直接使用 $r$ 和 $c$，因为有可能行列互换了）
5. 然后，按顺序沿着类似的思路，从第一行开始往下填充剩余的行。

时间复杂度

• 预处理的时间复杂度为 $O(n + m)$。
• 模拟填充的时间复杂度也为 $O(n + m)$。
• 故总时间复杂度为 $O(n + m)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储邻接表，度数和答案。

C++ 代码

#define LL long long

class Solution {
public:
    vector<vector<int>> constructGridLayout(int n, vector<vector<int>>& edges) {
        const int m = edges.size();
        vector<vector<int>> graph(n);
        vector<int> deg(n, 0);

        for (const auto &e : edges) {
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
            ++deg[e[0]]; ++deg[e[1]];
        }

        int r = (
                2 * n - m - 
                    sqrt(4ll * n * n - 4ll * m * n + (LL)(m) * m - 4 * n)
            ) / 2;

        int c = n / r;

        vector<vector<int>> ans;
        vector<int> used(n, false);
        if (r == 1) {
            ans.resize(1, vector<int>(c));

            for (int i = 0; i < n; i++)
                if (deg[i] == 1) {
                    ans[0][0] = i;
                    used[i] = true;

                    break;
                }

            for (int j = 1; j < c; j++) {
                for (int x : graph[ans[0][j - 1]])
                    if (!used[x]) {
                        ans[0][j] = x;
                        used[x] = true;

                        break;
                    }
            }
        } else if (r == 2) {
            ans.resize(2, vector<int>(c));

            for (int i = 0; i < n; i++)
                if (deg[i] == 2) {
                    ans[0][0] = i;
                    used[i] = true;

                    break;
                }

            for (int v : graph[ans[0][0]])
                if (deg[v] == 2) {
                    ans[1][0] = v;
                    used[v] = true;

                    break;
                }

            for (int j = 1; j < c; j++) {
                for (int i = 0; i < 2; i++)
                    for (int x : graph[ans[i][j - 1]])
                        if (!used[x]) {
                            ans[i][j] = x;
                            used[x] = true;

                            break;
                        }
            }
        } else {
            ans.push_back({});

            for (int i = 0; i < n; i++)
                if (deg[i] == 2) {
                    ans[0].push_back(i);
                    used[i] = true;

                    break;
                }

            int j = 1;
            bool end = false;
            while (!end) {
                for (int x : graph[ans[0][j - 1]])
                    if (!used[x] && deg[x] <= 3) {
                        ans[0].push_back(x);
                        used[x] = true;

                        if (deg[x] == 2)
                            end = true;

                        break;
                    }

                j++;
            }

            if (j == r)
                swap(r, c);

            ans.resize(r, vector<int>(c));

            for (int i = 1; i < r; i++)
                for (int j = 0; j < c; j++)
                    for (int x : graph[ans[i - 1][j]])
                        if (!used[x]) {
                            ans[i][j] = x;
                            used[x] = true;

                            break;
                        }
        }

        return ans;
    }
};