最长回文子串

题目描述

给定一个字符串，请你求出其中的最长回文子串的长度。

例如，给定字符串 Is PAT&TAP symmetric? ，最长回文子串为 s PAT&TAP s，其长度是 11
。

输入格式

包含一个非空字符串。

输出格式

输出一个整数，表示给定字符串的最长回文子串的长度。

数据范围

给定字符串的长度不超过 1000。

算法1(半径法)和算法2(DP) 的 T(n) 和 S(n) 对比 ，半径法远远优于DP(时间上相差了近20倍)

算法1

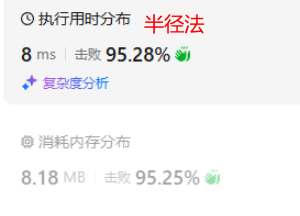
算法2

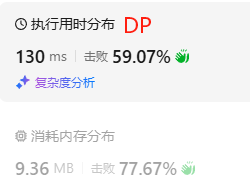
算法1

中心点找半径 $O(n^2)$

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 1010;

int main(){
    string s; 
    getline(cin, s);
    int res = 0 , q = 0 ;
    //int r_q , rr_q ; //若要求输出最长的回文子串，定义两个符号保存半径
    for(int i = 0; i < s.size(); i ++){
        //检查奇数回文子串--->只有一个起点
        int r = 1; //一个元素本身就是一个奇数回文子串 ， 所以初始化为1
        while(i - r >= 0 && i + r < s.size() && s[i - r] == s[i + r]) r ++ ;
        //while跳出时，r - 1 才是该回文串的半径
        //r_q = r - 1;//r_q保存奇数回文串的半径
        r = (r - 1) * 2 + 1 ;

        //检查偶数回文子串----->若有则有左右两个起点
        int rr = 0 ;//本身不是偶数回文子串，所以初始化为0
        if (i >= 0 && i + 1 < s.size() && s[i] == s[i + 1])//首先判断是否符合偶数回文子串
        {
            int rr_l = i , rr_r = i + 1 ; //偶数回文子串的左、右起点
            rr = 1 ;//半径初始化为1
            while (rr_l - rr >= 0 && rr_r + rr < s.size() && s[rr_l - rr] == s[rr_r + rr]) rr ++;
            //rr_q = rr ;//rr_q保存偶数回文子串的半径
            rr = rr * 2 ;//不需要rr - 1 ， while跳出时，rr 就是该偶数回文字串的半径
        }
        res = max(res , max(rr , r)) ;
        //每次比较时同时确定每次最长回文子串的半径
        // if (res < rr) { q = i - rr_q + 1 ; res = rr ; }
        // if (res < r)  { q = i - r_q ; res = r ; }
        if (res > (s.size() - i) * 2 ) break; //(关键特判)很省时间的一个特判 ， 能省去近一半的时间
    }
    //输出最长回文子串
    //cout << s.substr(q , res) << endl;

    cout << res << endl ;
}

算法2

最长回文子串(DP) $O(n^2)$

#include <iostream>

using namespace std;

bool f[1010][1010];

int main()
{
    string s ;
    getline (cin , s);

    int res = 0 , res_l , n = s.size();

    for (int i = n - 1; i >= 0; i--) 
   {
        for (int j = i; j < n; j++) 
       {
            if (i == j ) //判断边界，若是单个字符a，必是回文
            f[i][j] = true; 
            else if (i + 1 == j) //若两个字符相邻，f[i][j]状态更新看这两个字符是否相等
            f[i][j] = s[i] == s[j];
            else  //其他情况：若两字符相等，回文可以拓展，前提是子串也是回文
           {
            if (s[i] == s[j]) f[i][j] = f[i+1][j-1]; //若子串是回文也是回文，不是回文
           }

            if (f[i][j] && res < j - i + 1) 
            {
               res = j - i + 1 ;
               res_l = i ;
            }
       }
   }
    // cout << s.substr(res_l , res);
    cout << res << endl;

    return 0;
}
//DP思路from：卷卷死他们

算法3

(暴力枚举) $O(n^3)$ (会TLE)

#include <iostream>
#include <cstring>

using namespace std;

bool is_huiwen(string s , int l , int r)
{
    int mid = (r - l + 1) / 2 ;
    for (int i = 0 ; i < mid ; i ++)
        if (s[l + i] != s[r - i]) return false;
    return true;  
}

int main()
{
    string s ;
    getline(cin , s);
    int res = 0 , res_l , res_r , n = s.size();

    for (int i = 0 ; i < n ; i ++) // n
       for (int j = i ; j < n ; j ++ ) // n
         {
            if (is_huiwen(s , i , j)) // n
            {

                if (res < j - i + 1)
                {
                    res = j - i + 1;
                    res_l = i ;
                    res_r = j;   
                }
            }
          }

    //  cout << s.substr(res_l , res);

        cout << res << endl;  
        return 0 ;
}