题目描述

给你一棵 二叉树 的根节点 root 和一个整数 k。

返回第 k 大的 完美二叉 子树 的大小，如果不存在则返回 -1。

完美二叉树 是指所有叶子节点都在同一层级的树，且每个父节点恰有两个子节点。

子树 是指树中的某一个节点及其所有后代形成的树。

样例

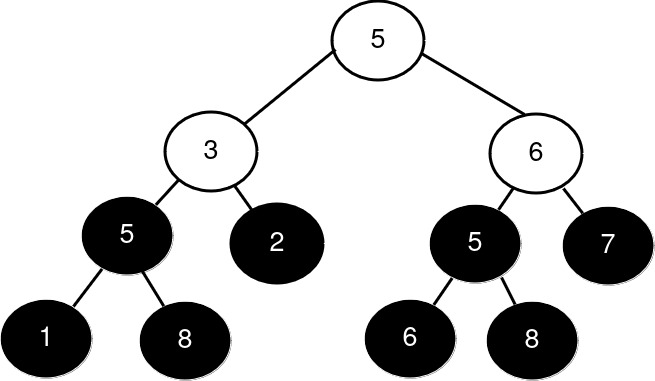
输入： root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2

输出： 3

解释：

完美二叉子树的根节点在图中以黑色突出显示。它们的大小按降序排列为 [3, 3, 1, 1, 1, 1, 1, 1]。
第 2 大的完美二叉子树的大小是 3。

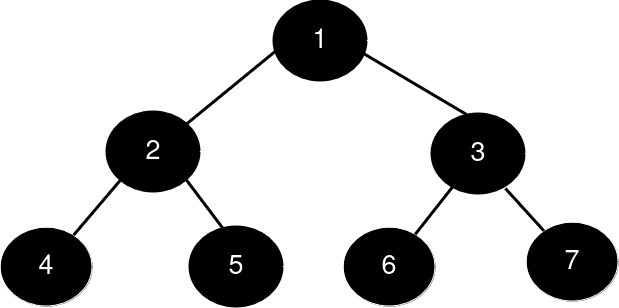
输入： root = [1,2,3,4,5,6,7], k = 1

输出： 7

解释：

完美二叉子树的大小按降序排列为 [7, 3, 3, 1, 1, 1, 1]。最大的完美二叉子树的大小是 7。

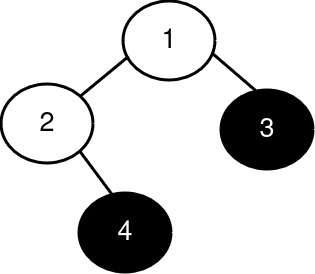
输入： root = [1,2,3,null,4], k = 3

输出： -1

解释：

完美二叉子树的大小按降序排列为 [1, 1]。完美二叉子树的数量少于 3。

限制

• 树中的节点数目在 [1, 2000] 范围内。
• 1 <= Node.val <= 2000
• 1 <= k <= 1024

算法

(深度优先遍历) $O(n)$

1. 对二叉树进行深度优先遍历。遍历过程中，返回子节点的高度以及是否子节点为完美二叉子树。
2. 如果两个子节点都是完美二叉子树，且高度一致，则当前节点也是完美二叉子树。
3. 遍历过程中收集所有的二叉子树的节点个数，最后找到第 $k$ 大的元素。

时间复杂度

• 遍历二叉树每个节点一次，寻找答案的时间复杂度也为 $O(n)$，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储所有合法的节点和递归的系统栈。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    vector<int> cnt;

    pair<int, bool> solve(TreeNode *u) {
        if (!u)
            return make_pair(0, true);

        TreeNode *l = u->left, *r = u->right;
        auto pl = solve(l);
        auto pr = solve(r);

        int h = max(pl.first, pr.first) + 1;
        bool perfect = pl.second && pr.second && pl.first == pr.first;

        if (perfect)
            cnt.push_back((1 << h) - 1);

        return make_pair(h, perfect);
    }

public:
    int kthLargestPerfectSubtree(TreeNode* root, int k) {
        solve(root);

        if (cnt.size() < k)
            return -1;

        k = cnt.size() - k;
        nth_element(cnt.begin(), cnt.begin() + k, cnt.end());

        return cnt[k];
    }
};