题目描述

求a^b的约数之和

需记忆的公式

一个数N = p1^a1 * p2^a2…… * pk^ak

约数个数 = (a1 + 1) * (a2 + 1) * (a3 + 1) …… (ak + 1)

约数之和 = (p1^0 + p1^1 + …… p1^a1) * (p2^0 + p2^1 …… p2^a2) …… (pk^0 + pk^1 …… pk^ak)

我们导入sum函数中的值sum(p, a + 1),到达函数sum(int p, int k),可在进行折半递归，证明公式如下
1.k为偶数时证明如下

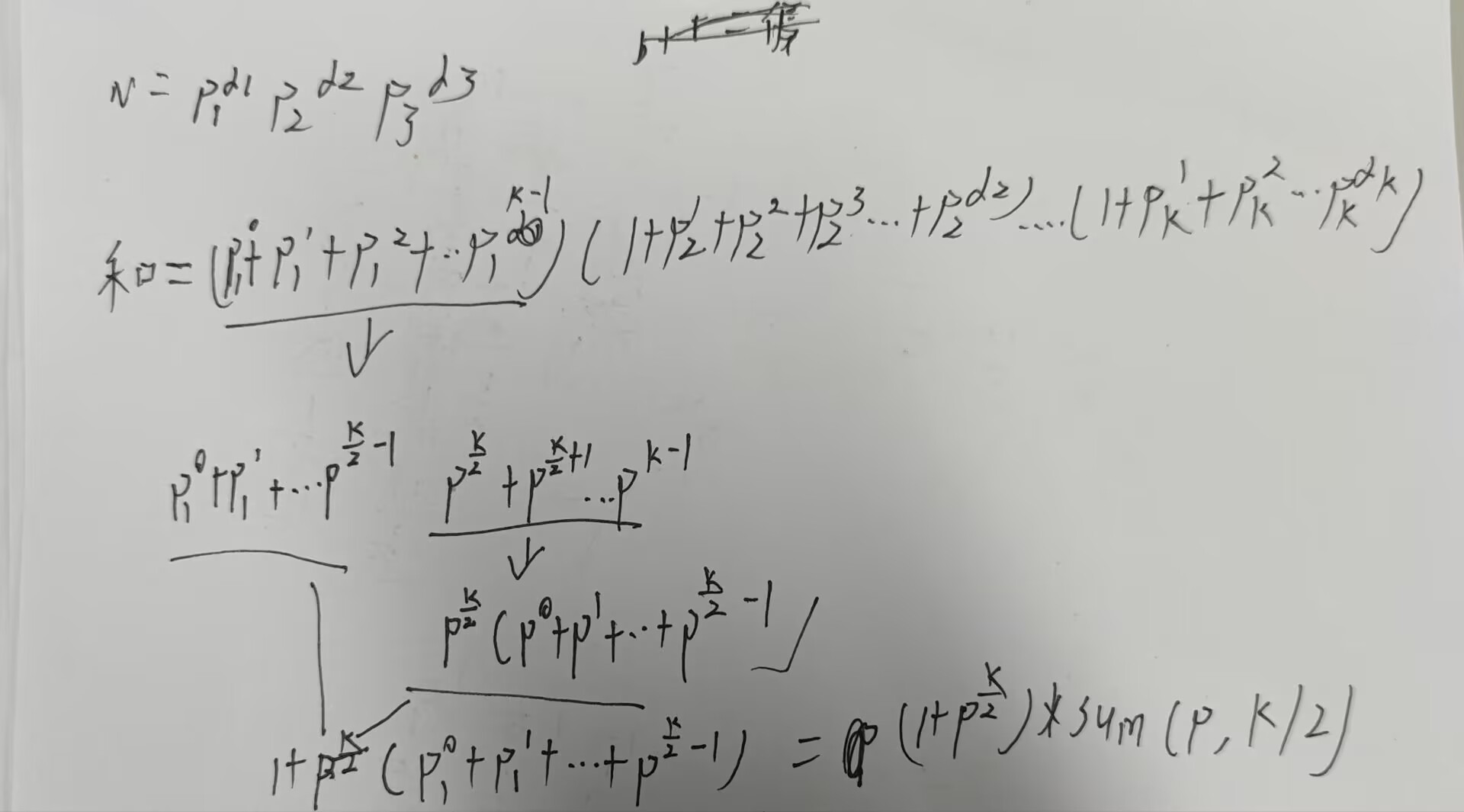
2.k为奇数时证明如下

另外要注意的是，本题要求算的是a^b的约数之和，a = (p1^e1) * (p2^e2) …… (pk^ek)
在求约数之和是可以将b作为指数带入公式(p1^0 + p1^1 + …… p1^a1) * (p2^0 + p2^1 …… p2^a2) …… (pk^0 + pk^1 …… pk^ak)， 变成(p1^(0 * b) + p1^(1 * b) + …… p1^(a1 * b)) * (p2^(0 * b) + p2^(1 * b) …… p2^(a2 * b)) …… (pk^(0 * b) + pk^(1 * b) …… pk^(ak * b))

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int mod = 9901;

int qmi(int a, int k)
{
    int res = 1;
    a %= mod;
    while (k)
    {
        if (k & 1) res = res * a % mod;
        k >>= 1;
        a = a * a % mod;
    }

    return res;
}

int sum(int p, int k)
{
    if (k == 1) return 1;
    //传入进来的是s + 1，真实a(阿尔法)实则是k - 1
    if (k % 2 == 0) return (1 + qmi(p, k / 2)) * sum(p, k / 2) % mod;
    return (sum(p, k - 1) + qmi(p, k - 1)) % mod;
}

int main()
{
    int a, b;
    cin >> a >> b;
    int res = 1;
    for (int i = 2; i <= a / i; i ++ )
        if (a % i == 0)
        {
            int s = 0;
            while (a % i == 0)
                s ++, a /= i;
            res = res * sum(i, s * b + 1) % mod;
        }

    if (a > 1) res = res * sum(a, b + 1) % mod;
    if (a == 0) res = 0;

    cout << res;
}