题目描述

在图像编码的算法中，需要将一个给定的方形矩阵进行 $Z$ 字形扫描(Zigzag Scan)。

给定一个 $n×n$ 的矩阵，$Z$ 字形扫描的过程如下图所示：

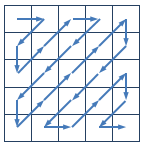
对于下面的 $4×4$ 的矩阵，

1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

对其进行 $Z$ 字形扫描后得到长度为 $16$ 的序列：1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3。

请实现一个 $Z$ 字形扫描的程序，给定一个$ n×n$ 的矩阵，输出对这个矩阵进行$ Z$字形扫描的结果。

输入格式

输入的第一行包含一个整数 $n$，表示矩阵的大小。

输入的第二行到第 $n+1$ 行每行包含$ n$ 个正整数，由空格分隔，表示给定的矩阵。

输出格式

输出一行，包含 $n×n$ 个整数，由空格分隔，表示输入的矩阵经过 $Z$ 字形扫描后的结果。

数据范围

$1≤n≤500$，矩阵元素为不超过 $1000$ 的正整数。

输入样例：

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

输出样例：

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

题目解析

曼哈顿距离 + 模拟

观察斜着打印的坐标的特点，可以发现直线方程都是$x + y = k$的形式，至于往下平移，$k$从小到大枚举即可最大$n^2$

那么打印的顺序观察$k$的奇偶性即可。

要注意的是，这里不是所有坐标都有值，要判断要打印的坐标是否合法

时间复杂度$O(n^3)$

C++代码

#include <bits/stdc++.h>

using namespace std;

const int N = 510;

int a[N][N];

int n;

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 1 ; j <= n ; j ++)
            cin >> a[i][j];


    for(int i = 2 ; i <= 2 * n ; i ++)
    {
        if(i % 2 == 0)
            for(int y = 1 ; y <= n ; y ++)
            {
                if(i - y <= 0 || i - y > n) continue;
                // cout << y << ' ' << i - y << '\n';
                cout << a[i - y][y] << ' ';
            }

        else 
            for(int x = 1 ; x <= n; x ++)
            {
                if(i - x <= 0 || i - x > n) continue;
                // cout << x << ' ' << i - x << '\n';
                cout << a[x][i - x] << ' ';
            }

    }
    return 0;
}