第一种解法

这种解法参考了全排序题目，具体思路是：
dfs每一行，遍历每行的第几列放皇后
例如：1,3,_, _表示：第一行1列，第二行3列放了皇后，剩下两列等待递归。
这里需要存储的信息是每列，每个左对角线，每个右对角线是否都放了皇后

有个重要的问题：怎么表示每条对角线是否放了皇后呢？
先上个图：

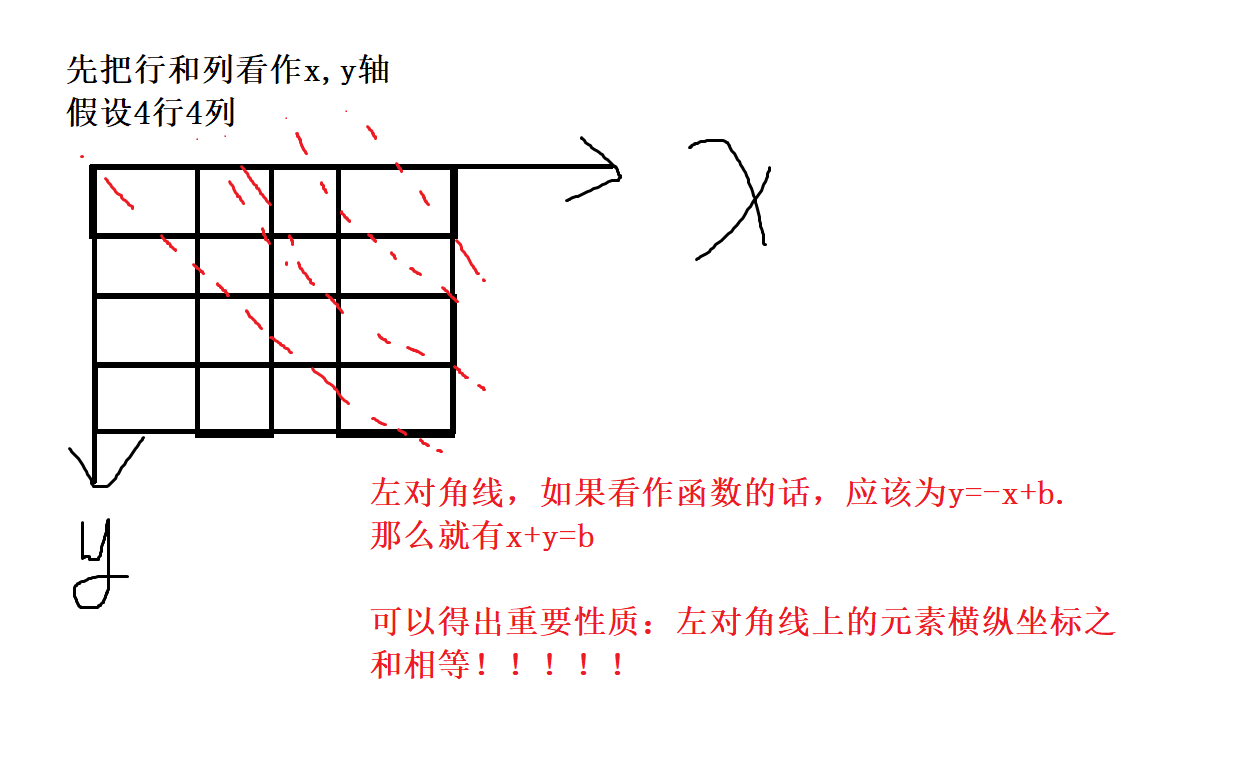
我们可以得出，左对角线上元素横纵坐标之和相等！
同理，右对角线上的元素满足横纵之差相等。
但是，作差可能会有越界问题，所以我们最后整体加上n，防止越界

#include <iostream>
#include <cstring>
#include <algorithm>
//参考全排列的思想，把每一行看作一个空格，空格填的数字就是皇后在当前行的多少列

using namespace std;

const int N = 10;

int n;
char board[N][N];//存储当前棋盘的状态
bool col[N],rtol[N*2],ltor[N*2];//rtol是从右到左的对角线，ltor同理
//对角线怎么存储的？题解画图来理解

void dfs(int r)
{
    if(r==n)
    {
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                cout<<board[i][j];
            }
            cout<<endl;
        }
        cout<<endl;
        return;
    }
    //枚举某行中每一列的情况
    for(int i=0;i<n;i++)
    {
        if(!col[i]&&!rtol[r+i]&&!ltor[n+r-i])
        {
            col[i]=rtol[r+i]=ltor[n+r-i]=true;
            board[r][i]='Q';
            dfs(r+1);
            col[i]=rtol[r+i]=ltor[n+r-i]=false;
            board[r][i]='.';
        }
    }
}


int main()
{
    cin>>n;

    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            board[i][j]='.';
        }
    }


    dfs(0);
    return 0;
}

第二种解法

这是比较原始的方法了，就是每个格子每个格子的遍历。
每个格子分为放皇后和不放皇后两种情况来遍历
其它的与第一种方法差不多
代码中写了我犯错的地方，需要本人特别注意！

#include <iostream>
#include <cstring>
#include <algorithm>
//参考全排列的思想，把每一行看作一个空格，空格填的数字就是皇后在当前行的多少列

using namespace std;

const int N = 10;

int n;
char board[N][N];//存储当前棋盘的状态
bool row[N],col[N],rtol[N*2],ltor[N*2];//rtol是从右到左的对角线，ltor同理
//对角线怎么存储的？题解画图来理解

//x表示行，y表示列，cnt表示当前放了多少皇后
void dfs(int x,int y,int cnt)
{

    if(y>=n)
    {
        x++;
        y=0;
    }

    if(cnt>n) return;
    //第一次写成了(x==n&&cnt==n)，是因为没有考虑到cnt!=n的时候也必须要return,从而导致越界报错
    if(x==n)
    {
        if(cnt==n)
        {
            for(int i=0;i<n;i++)
            {
                for(int j=0;j<n;j++)
                {
                    cout<<board[i][j];
                }
                cout<<endl;
            }
            cout<<endl;

        }
        return;

    }
    //枚举每个格子的情况

    //不放
    dfs(x,y+1,cnt);

    //放
    if(!row[x]&&!col[y]&&!rtol[x+y]&&!ltor[n+x-y])
    {
        row[x]=col[y]=rtol[x+y]=ltor[n+x-y]=true;
        board[x][y]='Q';
        dfs(x,y+1,cnt+1);
        board[x][y]='.';
        row[x]=col[y]=rtol[x+y]=ltor[n+x-y]=false;
    }

}


int main()
{
    cin>>n;

    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            board[i][j]='.';
        }
    }


    dfs(0,0,0);
    return 0;
}