蒟蒻想要个免费的赞，求求了

首先这个题大致思路是二分，我们通过二分寻找答案，左边的点是不满足的，右边的点是全部满足的

接着搬出方差另一种计算方式

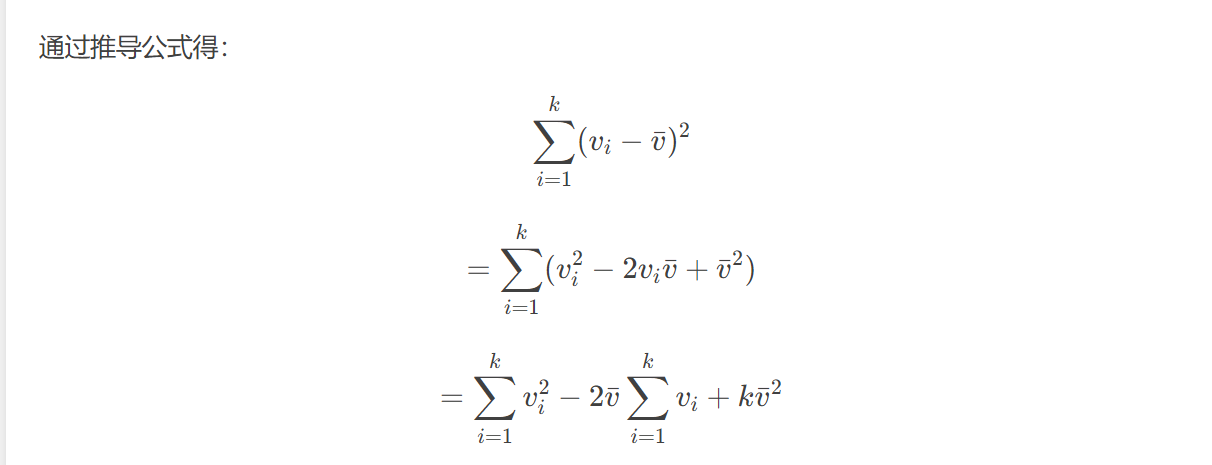
通过这里发现，我们只要处理前mid个数中，选k个数的总和与平方总和即可

这看起来很难处理，但我们只要排个序，那这k个数必然是连续的（因为方差反映离散程度，肯定是越集中越好）

那既然是维护连续k个数的信息，想必大家都知道这个是滑动窗口的典型应用

至此，问题得到完美的解决，代码如下

#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long

using namespace std;
const int N = 100010;

int n,k,T;
int a[N],b[N];
int mid;

bool check(int n){
    for(int i=1;i<=n;i++) b[i]=a[i];  //备份一份，用来进行处理
    sort(b+1,b+1+n);

    int vi2=0,vi=0;
    double avg;

    for(int i=1;i<k;i++) vi2+=b[i]*b[i],vi+=b[i];

    for(int i=k;i<=n;i++){

        vi2-=b[i-k]*b[i-k],vi-=b[i-k];     //滑动窗口记录每次平方和与总和，先弹出前面的
        vi2+=b[i]*b[i],vi+=b[i];           //在加入后面的

        avg = vi*1.0/k;
        if((vi2-2*avg*vi+k*avg*avg)/k<=T) return 1;   //符合条件

    }
    return 0;                       //不符合条件
}
signed main(){

    cin>>n>>k>>T;
    for(int i=1;i<=n;i++) cin>>a[i]; 

    if(!check(n)){                     //特判一下边界
        cout<<-1;
        return 0;
    }
    int l=k-1,r=n+1;
    while(l+1<r){                     //二分答案,最好背一个正确的板子
        mid=(l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid;
    }
    cout<<r;
    return 0;
}