[AcWing 1027] 方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

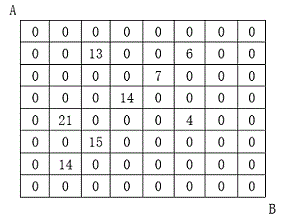
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N ≤ 10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

看到题目第一次想的是贪心做法，即走两遍dp，每次走当前最大的一条路，并且把走过的点置0，但并没有验证是否正确，并且答案也WA了

正确做法：三维dp

走一遍dp，只不过这一遍里面同时有两条路线在走

状态表示(f[k][i1][i2]):当前走 k 步，第一个人走到的位置横坐标是 i1， 第二个人走到的位置横坐标是 i2时，所获得的数的最大值。

算法步骤：

1. 第一个for循环枚举当前走的步数（k）
2. 第二个for循环枚举当前第一个人所走到位置的横坐标（i1）
3. 第三个for循环枚举第二个人所走到位置的横坐标（i2)

由题意，只能向右或向下走，故走到一个点的步数即该点的横纵坐标之和，由此得到：第一个人的坐标：(i1, k - i1)，第二个人的坐标：(i2,k - i2)，判断两人当前有没有重合，判断(i1 == i2)即可

接下来是确定状态转移方程：

当前走 k 步的状态 f[k][i][j] 均由前 k - 1 步转移而来，两人均走了一步，已知两人各有一种转移方式，即向右走或向下走，故一共有四种转移方式，即右右，右下，下右，下下（前一个表示第一个人的转移方式，后一个则为第二人）。

设两人当前走到位置获得的数的总和是sum，若两人不重合，则 sum = a[i1][k - i1] + a[i2][k - i2]；否则 sum = a[i1][k - i1] + 0。由此得到

状态转移方程： f[k][i1][j1] = max(f[k - 1][i1 - 1][i2 - 1], f[k - 1][i1 - 1][i2], f[k - 1][i1][i2 - 1], f[k][i1][i2]) + t;

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 15;

int n;
int g[N][N];
int f[N * 2][N][N];

int main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    int a, b, c;
    while(cin >> a >> b >> c, a || b || c) g[a][b] = c;

    for(int k = 1; k <= 2 * n; k ++){ // 总步数
        for(int i1 = 1; i1 <= n; i1 ++){ // 枚举 点1 横坐标
            for(int i2 = 1; i2 <= n; i2 ++){ // 枚举 点2 横坐标
                int j1 = k - i1, j2 = k - i2; // 分别计算两点纵坐标
                if(j1 > 0 && j1 <= n && j2 > 0 && j2 <= n){
                    int t = g[i1][j1];
                    if(i1 != i2) t += g[i2][j2]; // 两点不重合，若重合，则该点的值只能用一次
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); // 下下
                    x = max(x, f[k - 1][i1 - 1][i2] + t); // 下右
                    x = max(x, f[k - 1][i1][i2 - 1] + t); // 右下
                    x = max(x, f[k - 1][i1][i2] + t); // 右右
                }
            }
        }
    }
    cout << f[n * 2][n][n] << '\n';
    return 0;
}