前言

本篇着重解答自己在思考这道题中遇到的各种疑惑,希望通过题解的方式来记录一下,也希望对大家有所帮助,也欢迎大家在评论区探讨和指正.共勉

d数组和cnt数组的含义：

1. cnt[i]=x表示某个(源)点 到 i点 最短路径的边数为x
2. d[i]=x 表示某个(源)点 到 i点 最短路径为x

spfa判断负环的核心：

• 如果是不存在负环的有向图，假设 i点 到 j点的最短路径 已经确定了，顶点数是n 那么它的边数一定是n-1 因为不存在负环=>不可能往回走，或者说 路径上的点不可能重复
• 那么如果 某点 到 某点 最短路径 上的顶点数为n 但是边数>=n 那么根据 抽屉原理 一定是某点重复了
  或者说 往后走了 所以一定存在负环
  {抽屉原理：“如果每个抽屉代表一个集合，每一个苹果代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素”}
• 所以我们可以发现 还有优化的空间 因为整个有向图的顶点数是n
  但是存在这种情况：整个有向图中 某一点 到 某一点 的最短路径上的顶点数是m (假设n大于m) 根据上面 spfa判断负环的核心,只需要判断 这条最短路径上的边数 是否>=m就可以了 当然,用 边数>=n 来判断当然也可以，因为n是大于m的 但是这样会多走n-m边(毕竟是负环嘛~ 如果不设置条件 会一直在负环上转)

1.为什么d数组不需要初始化为0x3f3f3f3f?

答：没必要，d数组默认初始化为0 或者 任何一个数，把1~n点先加进来队列,遍历完这1~n点,队列里剩下的就是 负边的点(因为负边+初始设置的值一定会更小),负边是组成负环的必要条件，沿着这几个负边去找负环就可以了

2.为什么需要把1~n点先加进来队列?

答：遍历完这1~n点，也就是遍历整个有向图中的每一条边，把负边的点 加入队列中，负边是组成负环的必要条件，沿着这几个负边去找负环就可以了;
简单来说：遍历每一条边，找出所有负边，把点放入队列中

更新d[j]和cnt[j]时,模拟情况,如图所示：

假设有两条最短路径m和n(m0到t1 和 n0到t2),t1和t2都在队列中

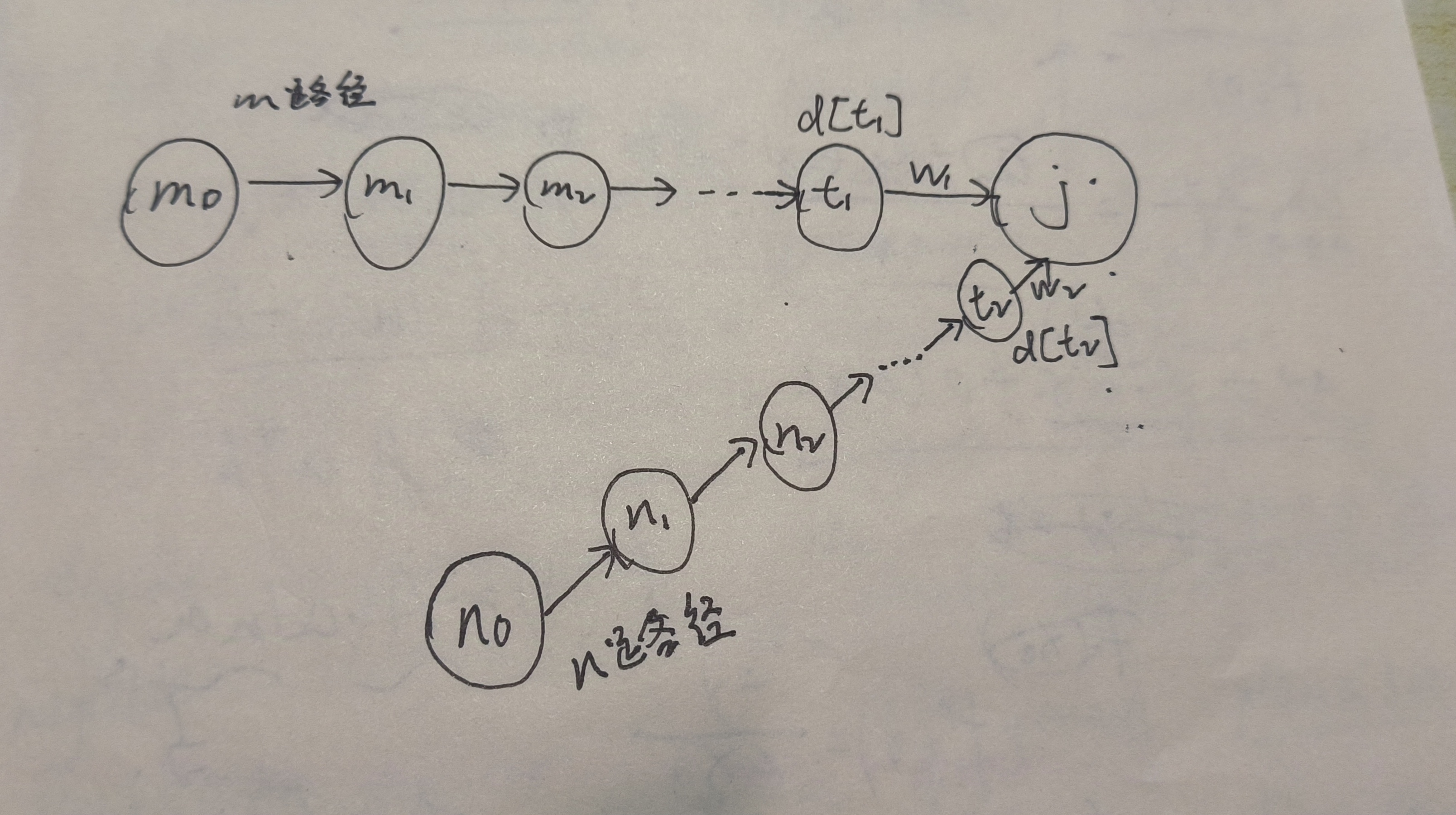
那么把队列中的t1和t2遍历完后，j点会选择m和n最短路径最小的加入(也就是d[t1]+w1和d[t2]+w2最小的)
注意：如果m或者n路径出现负环 那么根本到不了j这个点，因为一旦出现负环，便会一直在负环里面转下去，直到 这条最短路径上的边数>=n

通过模拟情况我想要强调的是

j选择的路径会改变,可能上一次还是m路径，过几次就是n路径了，但是！不管是哪条路径，都不妨碍我们找到负环

对照代码

#include<iostream>
#include<cstring>
#include<queue>

using namespace std;

const int N=10010;

int h[N],e[N],ne[N],w[N],idx;
bool st[N];
int d[N],cnt[N];
int n,m;
void add(int a,int b,int c){
    w[++idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx;
}

bool spfa(){
    queue<int>q;
    memset(d,0x3f,sizeof d);
    for(int i=1;i<=n;i++){
        q.push(i);
        st[i]=true;
    }
    while(q.size()){
        auto t=q.front();
        q.pop();
        st[t]=false;
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            if(d[j]>d[t]+w[i]){
                d[j]=d[t]+w[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n) return true;
                if(!st[j]){
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    return false;
}
int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    if(spfa()) puts("Yes");
    else puts("No");
}