【模板】Pollard-Rho
题目描述
Miller Rabin 算法是一种高效的质数判断方法。虽然是一种不确定的质数判断法,但是在选择多种底数的情况下,正确率是可以接受的。
Pollard rho 是一个非常玄学的方式,用于在 $O(n^{1/4})$ 的期望时间复杂度内计算合数 $n$ 的某个非平凡因子。事实上算法导论给出的是 $O(\sqrt p)$,$p$ 是 $n$ 的某个最小因子,满足 $p$ 与 $n/p$ 互质。但是这些都是期望,未必符合实际。但事实上 Pollard rho 算法在实际环境中运行的相当不错。
这里我们要写一个程序,对于每个数字检验是否是质数,是质数就输出 Prime;如果不是质数,输出它最大的质因子是哪个。
输入格式
第一行,$T$ 代表数据组数(不大于 $350$)
以下 $T$ 行,每行一个整数 $n$,保证 $2 \le n \le {10}^{18}$。
输出格式
输出 $T$ 行。
对于每组测试数据输出结果。
样例 #1
样例输入 #1
6
2
13
134
8897
1234567654321
1000000000000
样例输出 #1
Prime
Prime
67
41
4649
5
提示
2018.8.14 新加数据两组,时限加大到 2s,感谢 @whzzt
2022.12.22 加入新的数据,感谢 @ftt2333 和 Library Checker
by @will7101
算法1
(Pollard-Rho) $O(n^{1/4})$
1.1 问题的引入
给定一正整数 $N \in \mathbb{N}^*$,试快速找到它的一个因数。
很久很久以前,我们曾学过试除法来解决这个问题。很容易想到因数是成对称分布的:即 $N$ 的所有因数可以被分成两块:$[1, \sqrt{N}]$ 和 $[\sqrt{N}, N]$。这个很容易想清楚,我们只需要把区间 $[1, \sqrt{N}]$ 扫一遍就可以了,此时试除法的时间复杂度为 $O(\sqrt{N})$。
对于 $N \geq 10^{18}$ 的数据,这个算法运行起来无疑都是非常糟糕的。我们希望有更快的算法,比如 $O(1)$ 级别的?
对于这样的算法,一个比较好的想法是去设计一个随机程序,随便猜一个因数。如果你运气好,这个程序的时间复杂度下限为 $o(1)$。但对于一个 $N \geq 10^{18}$ 的数据,这个算法给出答案的概率是 $\frac{1}{10^{18}}$。当然,如果在 $[1, \sqrt{N}]$ 里面猜,成功的可能性会更大。
那么,有没有更好的改进算法来提高我们猜的准确率呢?
2.1 用一个悖论来提高成功率
我们来考虑这样一种情况:在 $[1, 1000]$ 里面取一个数,取到我们想要的数(比如说,$42$),成功的概率是多少呢?显然是 $\frac{1}{1000}$。
一个不行就取两个吧:随便在 $[1, 1000]$ 里面取两个数。我们想办法提高准确率,就取两个数的差值绝对值。也就是说,在 $[1, 1000]$ 里面任意选取两个数 $i, j$,问 $|i - j| = 42$ 的概率是多大?答案会扩大到 $\frac{1}{500}$ 左右,也就是将近扩大一倍。机房的gql大佬给出了简证:$i$ 在 $[1, 1000]$ 里面取出一个正整数的概率是 $100\%$,而取出 $j$ 满足 $|i - j| = 42$ 的概率差不多就是原来的一倍:$j$ 取 $i - 42$ 和 $i + 42$ 都是可以的。
这给了我们一点启发:这种“组合随机采样”的方法是不是可以大大提高准确率呢?
这个便是生日悖论的模型了。假如说一个班上有 $k$ 个人,如果找到一个人的生日是4月2日,这个概率的确会相当低。但是如果单纯想找到两个生日相同的人,这个概率是不是会高一点呢?可以暴力证明:如果是 $k$ 个人生日互不相同,则概率为:
$p = \frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \cdots \cdot \frac{365 - k + 1}{365}$
故生日有重复的现象的概率是:
$P(k) = 1 - \prod_{i=1}^{k} \frac{365 - i + 1}{365}$
我们随便取一个概率:当 $P(k) \geq \frac{1}{2}$ 时,解得 $k \approx 23$。这意味着一个有23个人组成的班级中,两个人在同一天生日的概率至少有 $50\%$!当 $k$ 取到60时,$P(k) \approx 0.9999$。这个数学模型和我们日常的经验严重不符。这也是“生日悖论”这个名字的由来。
3.1 随机算法的优化
生日悖论的实质是:由于采用“组合随机采样”的方法,满足答案的组合比单个个体要多一些。这样可以提高正确率。
我们不妨想一想:如何通过组合来提高正确率呢?有一个重要的想法是:最大公约数一定是某个数的约数。也就是说,$\forall k \in \mathbb{N}^*, \gcd(k, n) \mid n$。只要选适当的 $k$ 使得 $\gcd(k, n) > 1$ 就可以求得一个约数 $\gcd(k, n)$。这样的 $k$ 数量还是蛮多的:$k$ 有若干个质因子,而每个质因子的倍数都是可行的。
我们不放选取一组数 $x_1, x_2, x_3, \ldots, x_n$,若有 $\gcd(|x_i - x_j|, N) > 1$,则称 $\gcd(|x_i - x_j|, N)$ 是 $N$ 的一个因子。早期的论文中有证明,需要选取的数的个数大约是 $O(N^{1/4})$。但是,我们还需要解决储存方面的问题。如果 $N = 10^{18}$,那么我们也需要取 $10^4$ 个数。如果还要 $O(n^2)$ 来两两比较,时间复杂度又会弹回去。
3.2 Pollard Rho 和他的随机函数
我们不妨考虑构造一个伪随机数序列,然后取相邻的两项来求gcd。为了生成一串优秀的随机数,Pollard设计了这样一个函数:$f(x) = (x^2 + c) \mod N$ 其中 $c$ 是一个随机的常数。
我们随便取一个 $x_1$,令 $x_2 = f(x_1)$,$x_3 = f(x_2)$,……,$x_i = f(x_{i-1})$。在一定的范围内,这个数列是基本随机的,可以取相邻两项作差求gcd。
生成伪随机数的方式有很多种。但是这个函数生成出来的伪随机数效果比较好。它的图像长这个样子:
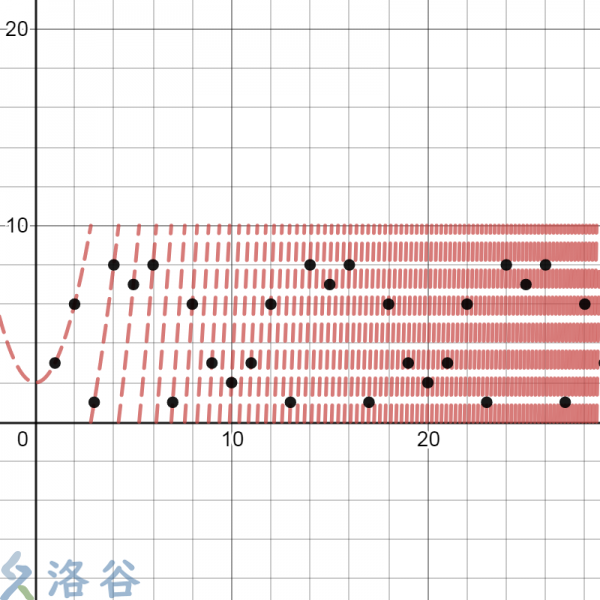
这里的函数为 $f(x) = (x^2 + 2) \mod 10$。图中的黑点为迭代 $1, 2, \ldots, 30$ 次得到的随机数。其实从这里很容易看出一个重复3次的循环节。
选取这个函数是自有道理的。有一种几何图形叫做曼德勃罗集,它是用 $f(x) = x^2 + c$,然后带入复数,用上面讲到的方式进行迭代的。png2 ↑曼德勃罗集。每个点的坐标代表一个复数 $x_1$,然后根据数列的发散速度对这个点染色。
这个图形和所谓的混沌系统有关。我猜大概是混沌这个性质保证了Pollard函数会生成一串优秀的伪随机数吧。
不过之所以叫伪随机数,是因为这个数列里面会包含有“死循环”。
$1, 8, 11, 8, 11, 8, 11, \ldots$ 这个数列是 $c = 7, N = 20, x_1 = 1$ 时得到的随机数列。这个数列会最终在8和11之间不断循环。循环节的产生不难理解:在模$N$意义下,整个函数的值域只能是 $0, 1, 2, \ldots, N-1$。总有一天,函数在迭代的过程中会带入之前的值,得到相同的结果。生成数列的轨迹很像一个希腊字母 $\rho$,所以整个算法的名字叫做Pollard Rho。
3.3 基于Floyd算法优化的Pollard Rho
为了判断环的存在,可以用一个简单的Floyd判圈算法,也就是“龟兔赛跑”。假设乌龟为 $t$,兔子为 $r$,初始时 $t = r = 1$。假设兔子的速度是乌龟的一倍。过了时间 $i$ 后,$t = i$,$r = 2i$。此时两者得到的数列值 $x_t = x_i$,$x_r = x_{2i}$。假设环的长度为 $c$,在环内恒有 $x_i = x_{i+c}$。如果龟兔“相遇”,此时有 $x_r = x_t$,也就是 $x_i = x_{2i} = x_{i+kc}$。此时两者路径之差正好是环长度的整数倍。
这样以来,我们得到了一套基于Floyd判圈算法的Pollard Rho 算法。
3.4 基于路径倍增和一个常数的优化
由于求 $\gcd$ 的时间复杂度是 $O(\log N)$ 的,频繁地调用这个函数会导致算法变得异常慢。我们可以通过乘法累积来减少求 $\gcd$ 的次数。显然的,如果 $\gcd(a, b) > 1$,则有 $\gcd(ac, b) > 1$,$c$ 是某个正整数。更进一步的,由欧几里得算法,我们有 $\gcd(a, b) = \gcd(ac \mod b, b) > 1$。我们可以把所有测试样本 $|t - r|$ 在模 $N$ 意义下乘起来,再做一次 $\gcd$。选取适当的相乘个数很重要。
我们不妨考虑倍增的思想:每次在路径 $\rho$ 上倍增地取一段 $[2^k - 1, 2^k]$ 的区间。将 $2^k - 1$ 记为 $l$,$2^k$ 记为 $r$。取而代之的,我们每次取的 $\gcd$ 测试样本为 $|x_i - x_l|$,其中 $l \leq i \leq r$。我们每次积累的样本个数就是 $2^k - 1$ 个,是倍增的了。这样可以在一定程度上避免在环上停留过久,或者取 $\gcd$ 的次数过繁的弊端。
当然,如果倍增次数过多,算法需要积累的样本就越多。我们可以规定一个倍增的上界。
$127 = 2^7 - 1$,据推测应该是限制了倍增的上界。
一旦样本的长度超过了127,我们就结束这次积累,并求一次 $\gcd$。127 这个数应该是有由来的。在最近一次学长考试讲解中,128 似乎作为“不超过某个数的质数个数”出现在时间复杂度中。不过你也可以理解为,将“迭代7次”作为上界是实验得出的较优方案。如果有知道和 128 有关性质的大佬,欢迎在下方留言。
这样,我们就得到了一套完整的,基于路径倍增的Pollard Rho 算法。
C++ 代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<random>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
LL prime[15]={2,3,5,13,17,31,37};
mt19937_64 rng(time(0));
LL max_factor;
LL gcd(LL a,LL b)
{
return b?gcd(b,a%b):a;
}
LL qmi(LL a,LL b,LL p)
{
LL res=1;
while(b)
{
if(b&1)res=(__int128)res*a%p;
a=(__int128)a*a%p;
b>>=1;
}
return res;
}
bool M_R(LL n,LL a)
{
LL d=n-1,r=0;
while(!(d&1))
{
d>>=1;
r++;
}
LL k=qmi(a,d,n);
if(k==1)return true;
for(int i=0;i<r;i++)
{
if(k==n-1)return true;
k=(__int128)k*k%n;
}
return false;
}
bool isprime(LL n)
{
if(n<=1)return false;
for(int i=0;i<7;i++)
{
if(n==prime[i])return true;
if(n%prime[i]==0)return false;
if(!M_R(n,prime[i]))return false;
}
return true;
}
LL f(LL x,LL c,LL n)
{
return ((__int128)x*x+c)%n;
}
LL PR(LL n)
{
LL s=0,t=0,c=(rng()%(n-1)+n-1)%(n-1)+1;
int stp=0,goal=1;
LL val=1;
for(goal=1;;goal<<=1,s=t,val=1)
{
for(stp=1;stp<=goal;stp++)
{
t=f(t,c,n);
val=(__int128)val*abs(t-s)%n;
if(stp%127==0)
{
LL d=gcd(val,n);
if(d>1)return d;
}
}
LL d=gcd(val,n);
if(d>1)return d;
}
}
void fac(LL n)
{
if(n<=max_factor||n==1)return;
if(isprime(n))
{
max_factor=max(max_factor,n);
return;
}
LL p=n;
while(p>=n)p=PR(n);
while(n%p==0)n/=p;
fac(n),fac(p);
}
int main()
{
int T;
cin>>T;
while(T--)
{
LL n;
scanf("%lld",&n);
max_factor=0;
fac(n);
if(max_factor==n)puts("Prime");
else printf("%lld\n",max_factor);
}
return 0;
}

